Two cars A and B cross a point P with velocities 10m/s and 15m/s. After that they move with different uniform accelerations and the car A overtakes B with a speed of 25ms−1. What is velocity of B at that instant?
(a)20ms−1
(b)25ms−1
(c)30ms−1
(d)40ms−1
The correct Answer is:A
To solve the problem, we need to analyze the motion of both cars A and B.
1. Identify Initial Velocities:
- Car A crosses point P with an initial velocity uA=10m/s.
- Car B crosses point P with an initial velocity uB=15m/s.
2. Final Velocity of Car A:
- At the point where car A overtakes car B, its velocity is given as vA=25m/s.
3. Use the Equation of Motion:
- We will use the equation of motion v=u+at for both cars.
- For car A:
vA=uA+aAt⟹25=10+aAt⟹aAt=15⟹aAt=15
- For car B:
vB=uB+aBt⟹vB=15+aBt
4. Distance Covered by Both Cars:
- Since both cars cover the same distance when A overtakes B, we can set their distance equations equal to each other.
- Distance covered by A:
d=uAt+12aAt2=10t+12aAt2
- Distance covered by B:
d=uBt+12aBt2=15t+12aBt2
5. Equate the Distances:
- Setting the distances equal gives:
10t+12aAt2=15t+12aBt2
- Rearranging gives:
12aAt2−12aBt2=5t
- Factoring out t (assuming t≠0):
12(aA−aB)t=5⟹aA−aB=10t
6. Substituting aAt:
- From step 3, we have aAt=15, so:
aA=15t
- Substitute into the equation:
15t−aB=10t⟹aB=15t−10t=5t
7. Finding Velocity of Car B:
- Now substitute aB back into the equation for vB:
vB=15+aBt=15+5=20m/s
Final Answer:
The velocity of car B at the instant when car A overtakes it is 20m/s.
- Car A crosses point P with an initial velocity uA=10m/s.
- Car B crosses point P with an initial velocity uB=15m/s.
- At the point where car A overtakes car B, its velocity is given as vA=25m/s.
- We will use the equation of motion v=u+at for both cars.
- For car A:
vA=uA+aAt⟹25=10+aAt⟹aAt=15⟹aAt=15
- For car B:
vB=uB+aBt⟹vB=15+aBt
- Since both cars cover the same distance when A overtakes B, we can set their distance equations equal to each other.
- Distance covered by A:
d=uAt+12aAt2=10t+12aAt2
- Distance covered by B:
d=uBt+12aBt2=15t+12aBt2
- Setting the distances equal gives:
10t+12aAt2=15t+12aBt2
- Rearranging gives:
12aAt2−12aBt2=5t
- Factoring out t (assuming t≠0):
12(aA−aB)t=5⟹aA−aB=10t
- From step 3, we have aAt=15, so:
aA=15t
- Substitute into the equation:
15t−aB=10t⟹aB=15t−10t=5t
- Now substitute aB back into the equation for vB:
vB=15+aBt=15+5=20m/s
The velocity of car B at the instant when car A overtakes it is 20m/s.
Topper's Solved these Questions
- KINEMATICS 1Book:DC PANDEY ENGLISHChapter:KINEMATICS 1Exercise:MCQ_TYPE
Explore 27 Videos
- KINEMATICS 1Book:DC PANDEY ENGLISHChapter:KINEMATICS 1Exercise:COMPREHENSION_TYPE
Explore 19 Videos
- KINEMATICSBook:DC PANDEY ENGLISHChapter:KINEMATICSExercise:INTEGER_TYPE
Explore 10 Videos
- LAWS OF MOTIONBook:DC PANDEY ENGLISHChapter:LAWS OF MOTIONExercise:Medical entrances gallery
Explore 39 Videos
Similar Questions
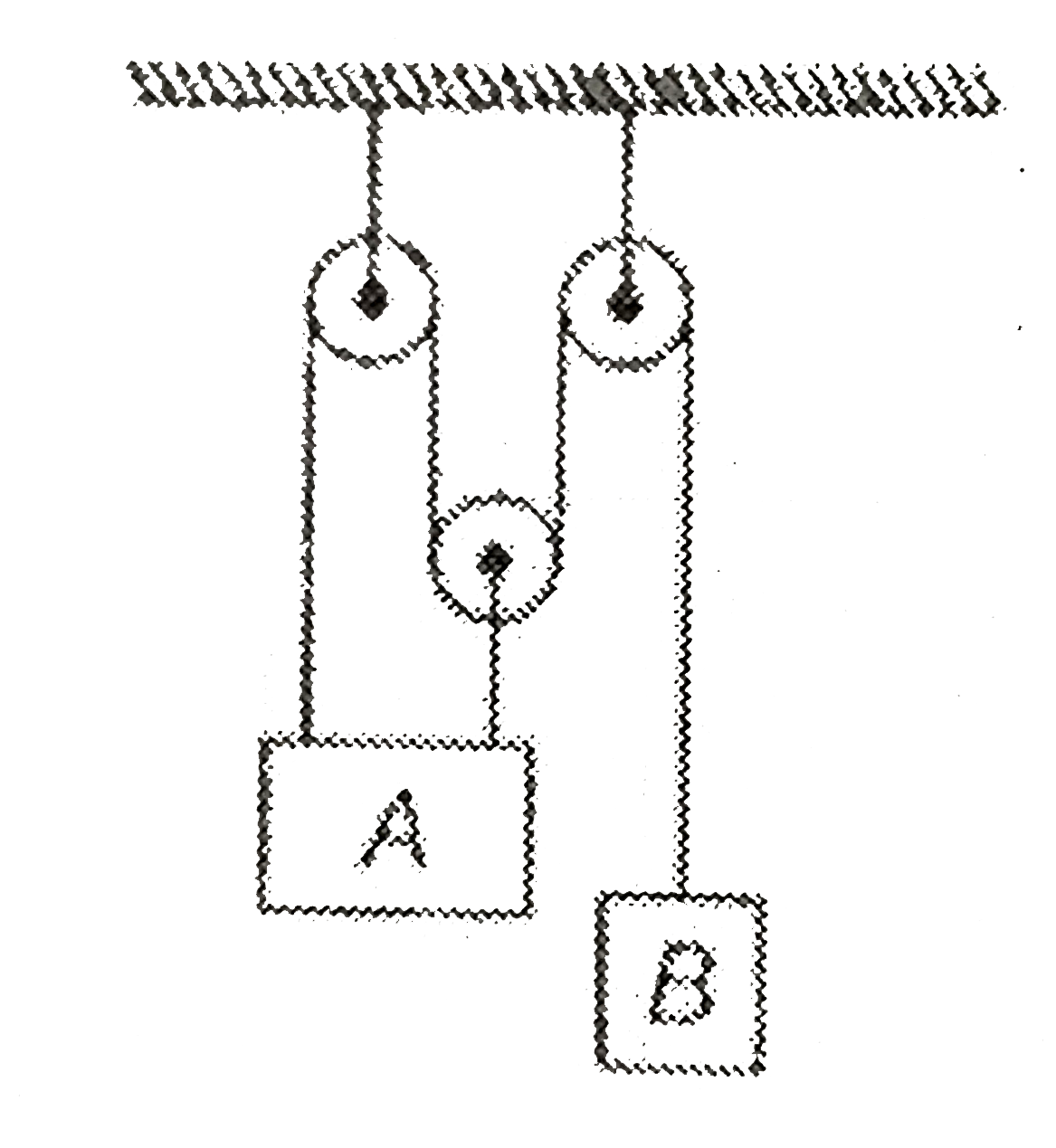
At a given instant. A is moving with velocity of 5m/s upward. What is velocity of B at that time:
View SolutionTwo cars X and Y start off to a race on a straight path with initial velocities of 8 m/s and 5 m/s respectively. Car X moves with uniform acceleration of 1m/s2 and car Y moves with uniform acceleration of 1.1m/s2. If both the cars reach the winning post together find the length of the track.
View SolutionTwo particles P and Q simultaneously start moving from point A with velocities 15m/s and 20m/s respectively. The two particles move with acceleration equal in magnitude but opposite in direction. When P overtakes Q at point B then its velocity is 30m/s, the velocity of Q at point B will be
View SolutionTwo cars a and B starts motion with a velocity of 10m/s and 20m/s respectively. Car a moves with a constant acceleration of 2.5m/s2 and car B have constant acceleration of 0.5m/s2 as shown in figure. Find when car A will over take car B. Dimension of car is negligible as compare to distance. Find the time after which car A over takes car B.
View SolutionTwo cars start off a race with velocities 2m/s and 4m/s travel in straight line with uniform acceleration 2m/s2and1m/s2 respectively. What is the length of the path if they reach the final point at the same time ?
View SolutionA car is moving in direction →r=−4ˆi+3ˆj with a speed of 10ms−1. Write the velocity vector of car in unit vector notation.
View SolutionA body is moving with uniform acceleration covers 200 m in the first 2 s and 220 m in the next 4s. Find the velocity in ms−1 after 7 s.
View SolutionTwo cars A and B are moving in same direction with velocities 30 m/s and 20 m/s. When car A is at a distance d behind the car B, the driver of the car A applies brakes producing uniform retardation of 2m/s2. There will be no collision when :-
View SolutionA particle moving along a straight line with uniform acceleration has velocities 7m/s at A and 17m/s at C. B is the mid point of AC. Then :-
View SolutionA car moving with constant acceleration crosses two points A and B with velocities 10 m/s and 20 m/s in its path. Find the velocity of the car midway between A and B. (in m/s).
View Solution

