Two balls of masses and and momenta and (in the directions shown) collide as shown in figure. During collsion, the value of linear impulse between them is J. In terms of J and p find coefficient of restitution 'e'. Under what condition collision is elastic. Also find the condition of perfectly inelastic collision.

The correct Answer is:A, B, C
Directions of linear impulses on the two colliding bodies at the time of collision are shown in fig.

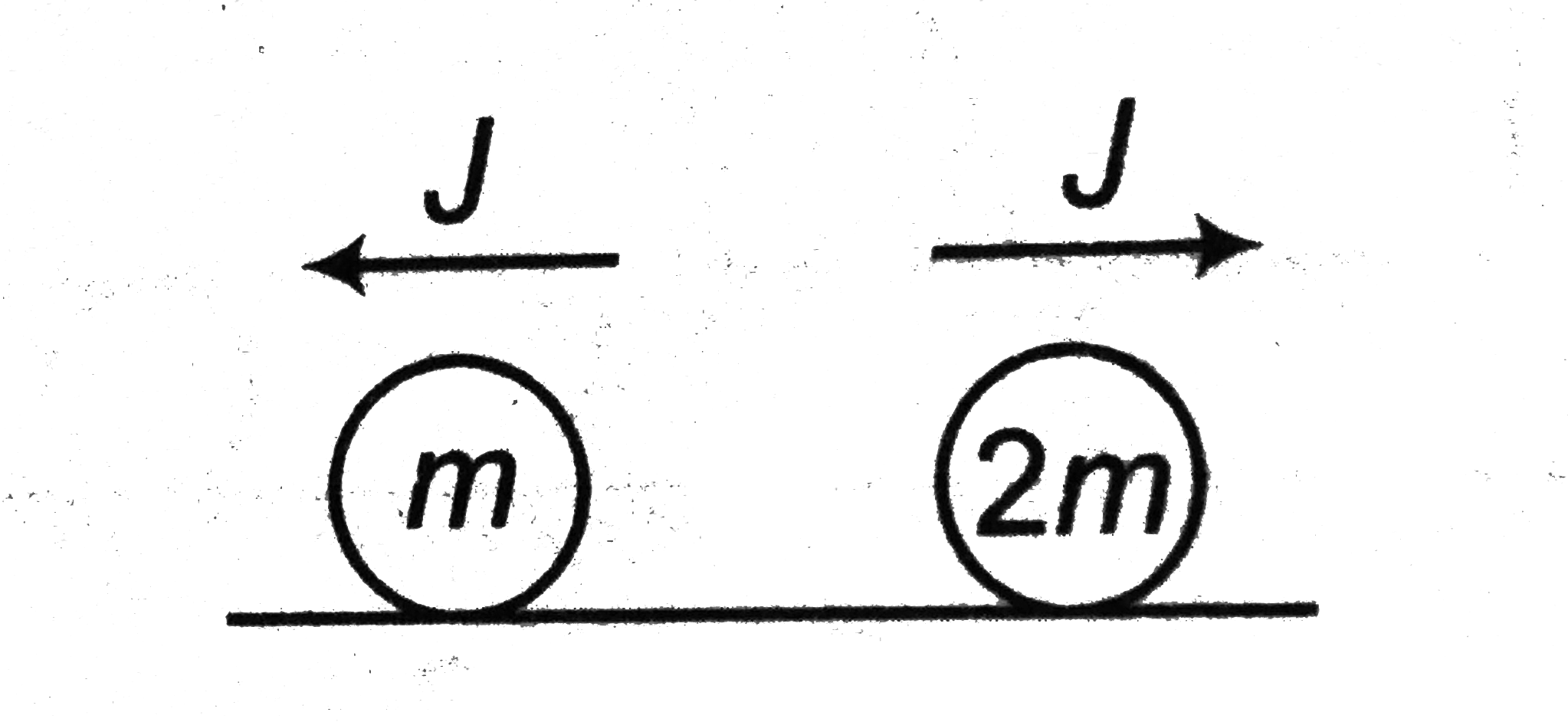

Linear impulse is equal to the change in linear momentum. Hence, momenta of the balls after collision are shown in figure.
Let and are their velocities before collision [in the directions shown in figure(a)] and and are the velocities after collision as shown in figure (c).
v=("linear momentum"/("mass")
e=("relative speed of separation")/("relative speed of approach")e=(v_1'+v_2')/(v_1+v_2)=((J-4p)/(m)+(J-2p)/(2m))/((4p)/(m)+(2p)/(2m))e=(3J-10p)/(10p)=(3J)/(10p)-1e=1rArr(3J)/(10p)=2J=(20)/(3p)e=0rArr(3J)/(10p)=1J=10/3p
Related Playlists
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - MiscellaneousExamples9videos
CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Exercise 11.113videos
CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Type 11videos
CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions15videos
CENTRE OF MASS, IMPULSE AND MOMENTUM
- BOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery19videos
CIRCULAR MOTION
Similar Questions
Two balls of masses m and 2m moving in opposite directions collide head on elastically with velocities v and 2v. Find their velocities after collision.
View SolutionTwo balls of masses m and 2m moving in opposite directions collide head on elastically with velocities v and 2v. Find their velocities after collision.
View SolutionA body X with a momentum p collides with another identical stationary body Y one dimensionally. During the collision, Y gives an impulse J to body X. Then coefficient of restitution is
View SolutionTwo bodies collide as shown in the diagram. During the collision , they exert impulse of magnitude J on each other

For what values of J(in N s) the 2 kg block will change its direction of velocity ?View SolutionTwo particles of masses m and 2m moving in opposite directions collide elastically with velocity 2v and v, respectiely. Find their velocities after collision.
 View Solution
View SolutionTwo balls of mass m and 2m each have momentum 2p and p in the direction shown in figure. During collision they exert an impulse of magnitude p on each other.

Column IColumn II(A)After collision momentum of m(p)2p(B)After collision momentum of 2m(q)p(C)Coefficient of restitution between them(r)1(s)NoneView SolutionA ball of mass m moving with speed u collides with a smooth horizontal surface at angle θ with it as shown in figure. The magnitude of impulse imparted to surface by ball is [Coefficient of restitution of collision is e]
 View Solution
View SolutionA glass ball collides with an identical ball at rest with v0=2 m/sec. If the coefficient of restitution of collision is e = 0.5, find the velocities of the glass balls just after the collision.
View SolutionTwo balls of mass m1 and m2 where m2=0.5m1, undergo head on collision as shown in figue.
_2019_CBT2_E01_005_Q01.png)
After collision the situation is as shown
_2019_CBT2_E01_005_Q02.png)
If V3=0.5v1. Value of V4 isView SolutionA ball moving with speed v collides with a horizontal smooth surface at an angle θ with normal to surface as shown in figure. If coefficient of restitution of collision is e, then find v'
 View Solution
View Solution


