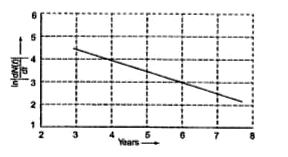
To determine the half life of radioactive elements, a student plots a graph of In ∣∣∣dN(t)dt∣∣∣ versus t. Here dN(t)dt the rate of radioactive decay at time t. If the number of radioactive nuclei of this element decreases dt by a factor of p after 4.16 years, find the value of p.
The correct Answer is:8
N=N0e−λt⇒dNdt=−λN0e−λt. Therefore ∣∣∣dNdt∣∣∣=λN0e−λt⇒ln∣∣∣dNdt∣∣∣=ln(λN0)−λt
The slope of the graph is =4−34−6=−12∴λ=12 per year.
Half life T1/2=0.6931/2=1.386 year
∴ Number of half lives =4.161.386=3, Hence p=(2)3=8
Similar Questions
To determine the half life of a radioactive element , a student plot a graph of in ∣∣∣dN(t)dt∣∣∣ versus t , Here ∣∣∣dN(t)dt∣∣∣ is the rate of radiation decay at time t , if the number of radioactive nuclei of this element decreases by a factor of p after 4.16year the value of p is
 View Solution
View SolutionTo determine the half life of a radioactive element , a student plot a graph of in ∣∣∣dN(t)dt∣∣∣ versus t , Here ∣∣∣dN(t)dt∣∣∣ is the rate of radiation decay at time t , if the number of radioactive nuclei of this element decreases by a factor of p after 4.16year the value of p is
 View Solution
View SolutionTo determine the half life of a radioactive element , a student plote a graph of in ∣∣∣dN(t)dt∣∣∣versust,Here∣∣∣dN(t)dt∣∣∣ is the rate of radioatuion decay at time t , if the number of radoactive nuclei of this element decreases by a factor of p after 4.16 year the value of p is
 View Solution
View SolutionThe t0.5 of a radioactive element is related to its average life by the expression
View SolutionDraw a graph showing the variation of decay rate (−dNdt) with number (N) of radioactive nuclei.
View SolutionThalassemia and sickle cell anemia are caued due to problem in globin molecule synthesis . Select the correct statement.
View SolutionThe half life of a radioactive substance is T0. At t=0,the number of active nuclei are N0. Select the correct alternative.
View SolutionThe half life of a radioactive element is T and its initial activity at t=0 is A0 and at t=t it is A, then
View SolutionIf −(dNdt)o is the initial activity and −(dNdt) is the activity at time t in a radioactive disintegration then :
View SolutionIf −(dNdt)o is the initial activity and −(dNdt) is the activity at time t in a radioactive disintegration then :
View Solution

