Time period of small oscillation (in a verical plane normal to the plane of strings) of the bob in the arrangement shown will be
_E01_023_Q01.png)
The correct Answer is:B
_E01_024_S01.png)
T=2π√l'g where l'=(l√2) so T=√l√2g
Related Playlists
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-0219videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise- 3 Match The Column1videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - SOME WORKED OUT EXAMPLES29videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)24videos
RACE
- BOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS4videos
TEST PAPER
Similar Questions
The time period of small oscillations of mass m :-
_S01_040_Q01.png) View Solution
View SolutionLet θ denote the angular displacement of a simple pendulum oscillating in a vertical plane. If the mass of the bob is m, the tension in the string is mgcosθ
View SolutionA simple pendulum suspended from the roof off a lift oscillates with frequency υ when the lift is at rest. If the lift falls freely under gravity, its frequency of oscillation becomes
View SolutionFind the time period of osciallation in the shown arrangement.
 View Solution
View SolutionTime period for small oscillations in vertical x - y plane of uniform semi - circular disk of mass m and radius R , about horizontal axis through point O, is equal to
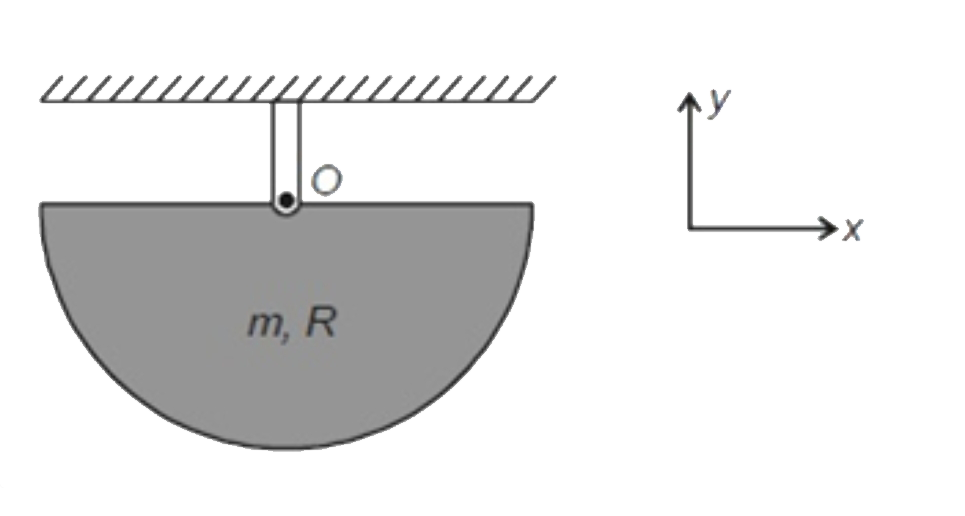 View Solution
View SolutionTwo light strings, each of length l are fixed at points A andB on a fixed horizontal and xy A small are making angle 45∘ with the bob if the bob is displaced normal to the plane of the string and released then period of the resulting small oscillation will be
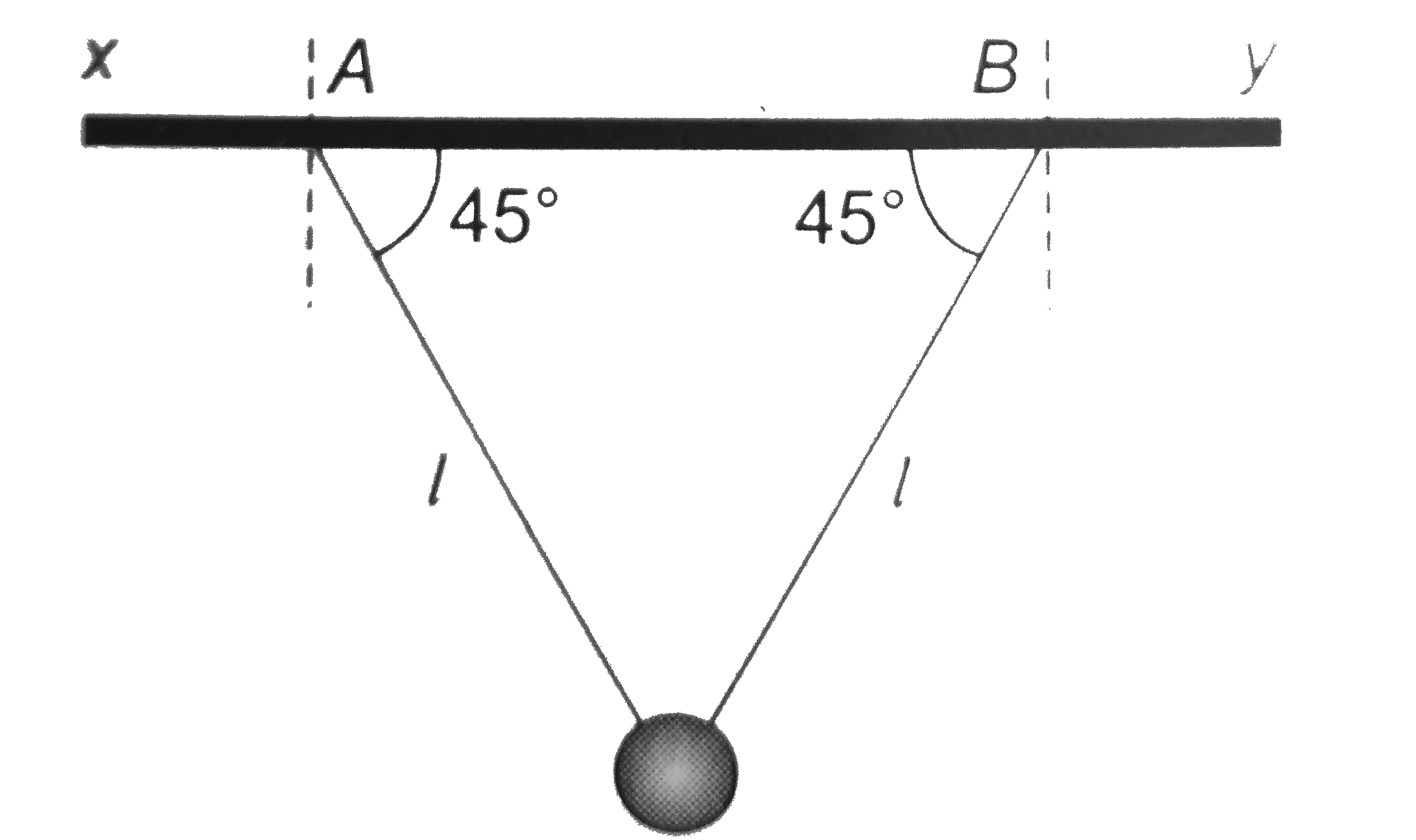 View Solution
View SolutionThe time period of oscillation of the block as shown in figure is
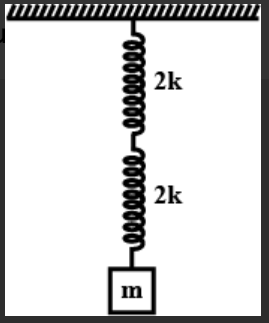 View Solution
View SolutionA: If a spring block system, oscillating in a vertical plane is made to oscillate on a horizontal surface, the time period will remain same.
R: The time period of spring block system does not depend on g.View SolutionWhat is the period of oscillation of a simple pendulum if its bob is made of ice ?
View SolutionThe bob of the pendulum shown in figure describes an arc of a circle in a vertical plane. If the tension in the cord is 2.5 times the weight of the bob for the position shown. Find the velocity and the acceleration of the bob in that position.
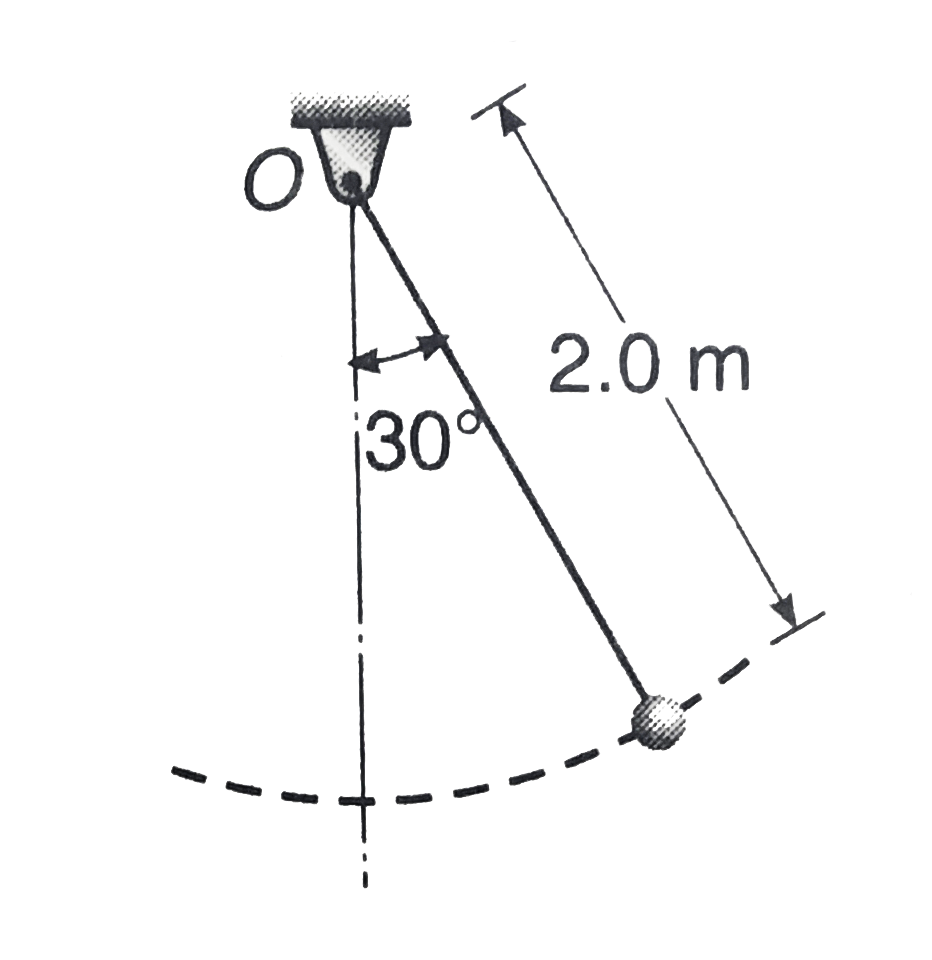 View Solution
View Solution


