Three vector as shown in (figure) have magnitudes |→a|=3,∣∣→b∣∣=4,and |→c|=10
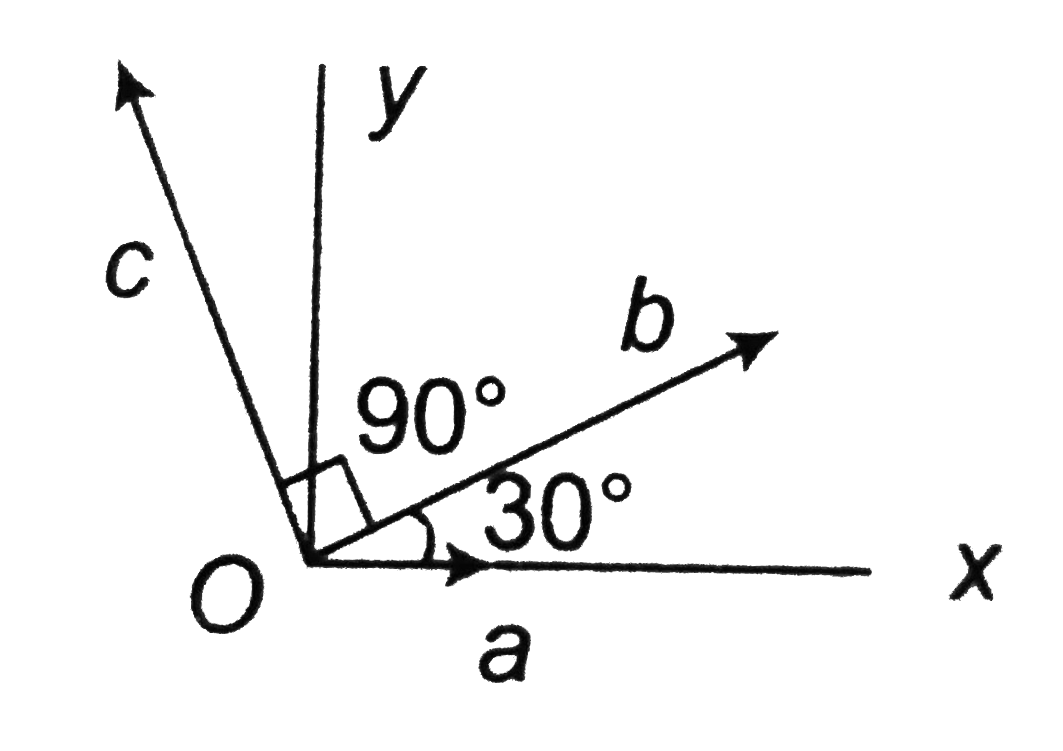
a.Find the x and y components of these vectors.
b.Find the numbers p and q such that →c=p→a+q→b.
The correct Answer is:a.ax=3,ay=0;bx;2√3;by=2;=−5;cy;=5√3;
b. q=5√32;p=−203
a.|→a|=3,∣∣→b∣∣=4,|→c|=10
ax=3,ay=0,
bx=bcos30∘=4×√32=2√3
by=4sin30∘4×√32=2√3
by=4sin30∘
=42=2,
cx=ccos120∘=−c×12=−102=−5,
cy=csin120∘=10×√32=5√3
b. Given c=P→a+q→b
cx=P→ax+q→bx⇒−5=3p+2√3q
cy=p→cy+q→by⇒5√3=0+2q⇒q=5√32
Replacing value of q,
−5=3p+2√3×5√32
or −5=3p+15 or p=−203
Topper's Solved these Questions
- VECTORSBook:CENGAGE PHYSICS ENGLISHChapter:VECTORSExercise:Exercise Single Correct
Explore 51 Videos
- VECTORSBook:CENGAGE PHYSICS ENGLISHChapter:VECTORSExercise:Exercise Multiple Correct
Explore 5 Videos
- VECTORSBook:CENGAGE PHYSICS ENGLISHChapter:VECTORSExercise:Exercise 3.2
Explore 13 Videos
- TRAVELLING WAVESBook:CENGAGE PHYSICS ENGLISHChapter:TRAVELLING WAVESExercise:Integer
Explore 9 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICS ENGLISHChapter:WORK, POWER & ENERGYExercise:Archives (integer)
Explore 4 Videos
Similar Questions
Knowledge Check
If →a,→b,→c are three vectors such that →a+→b+→c=0 and |→a|=2,∣∣→b∣∣=3,∣→c=5, then the value of →a.→b+→b.→c+→c.→a is
A0B1C38D−19The magnitude of the x-component of vector →A is 3 and the magnitude of vector →A is 5. What is the magnitude of the y-component of vector →A ?
A3B4C5D8
If two vectors →aand→b are such that ∣∣→a.→b∣∣=∣∣→a×→b∣∣, then find the angle the vectors →aand→b
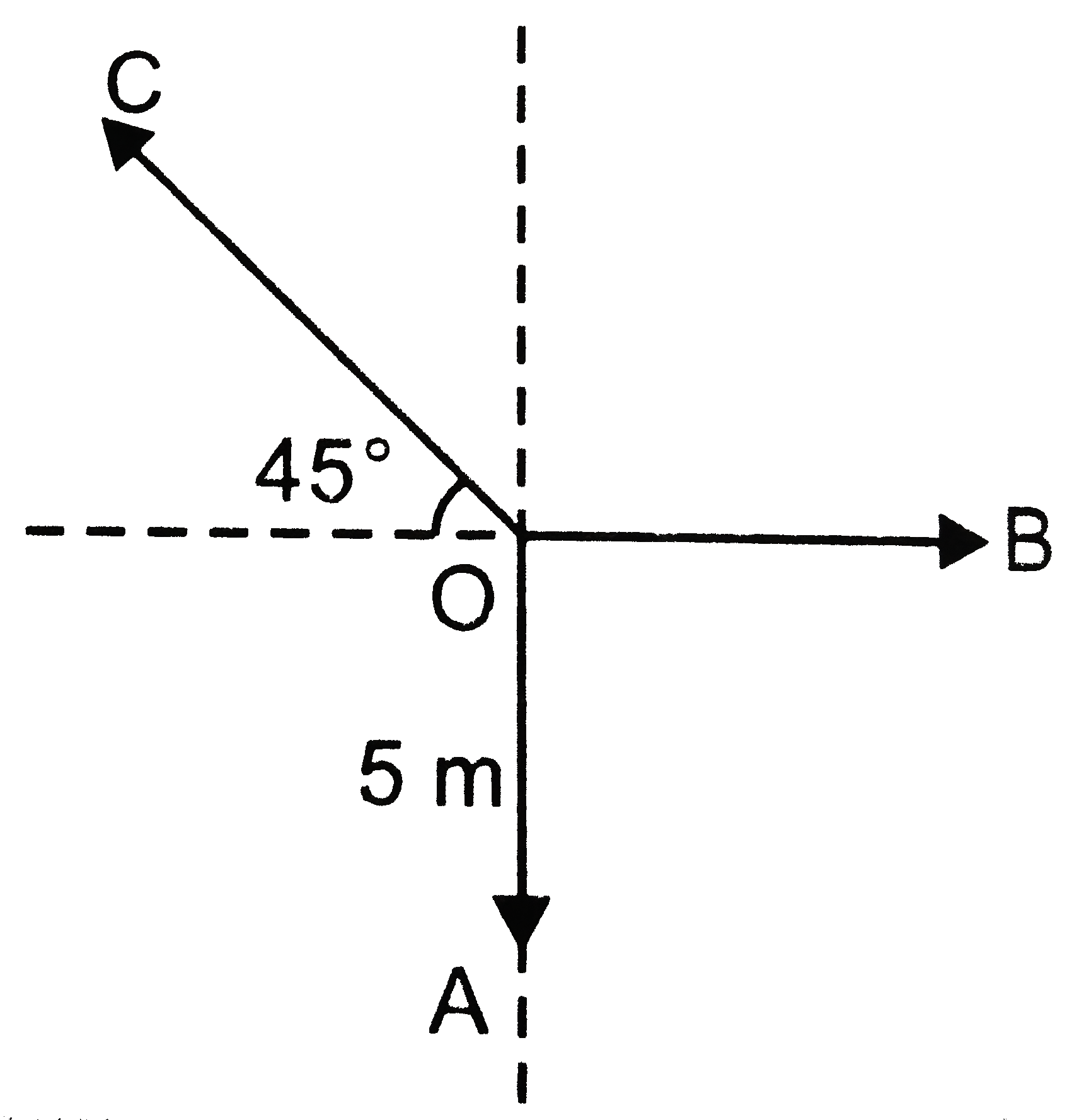
View SolutionThe sum of three vectors shown in Fig. 2 ( c) . 77. is zero .
 .
.
(a) What is the magnitude of the vector −−→OB?
(b) What is the magnitude of the vector −−→OC ?
View SolutionRefer to figure Find a the magnitude, b x and y components and c. the angle with the X-axis of the resultant of −−→OA,−−→BCand−−→DE.
 .
.
View SolutionVector →a,→b and →c are such that →a+→b+→c=→0 and |a|=3,∣∣→b∣∣=5 and |→c|=7. Find the angle between →a and →b .
View SolutionIf →a and →b are two vectors of the same magnitude inclined at an angle of 300 such that →a.→b=3, find |→a|,∣∣→b∣∣ .
View SolutionFind the angle between two vectors →aand →bwith magnitudes √3and 2 respectively having →a.→b=√6
View Solution

