Three particles of masses 1kg,32kg,and2kg are located the vertices of an equilateral triangle of side a. The x,y coordinates of the centre of mass are.
a. 5a9,2a3√3
b. 2a3√3,5a9
c. 5a9,2a√3
d. 2a√3,5a9
The correct Answer is:a
To find the coordinates of the center of mass of three particles located at the vertices of an equilateral triangle, we can follow these steps:
Step 1: Define the coordinates of the vertices
Let's place the three masses at the vertices of an equilateral triangle with side length a. We can assign the following coordinates to the vertices:
- Mass m1=1kg at (0,0)
- Mass m2=32kg at (a2,√32a)
- Mass m3=2kg at (a,0)
Step 2: Calculate the total mass
The total mass M of the system is given by:
M=m1+m2+m3=1+32+2=72kg
Step 3: Calculate the x-coordinate of the center of mass
The x-coordinate of the center of mass xcm is calculated using the formula:
xcm=m1x1+m2x2+m3x3M
Substituting the values:
xcm=(1)(0)+(32)(a2)+(2)(a)72
Calculating each term:
xcm=0+3a4+2a72=3a4+8a472=11a472=11a4⋅27=22a28=11a14
Step 4: Calculate the y-coordinate of the center of mass
The y-coordinate of the center of mass ycm is calculated similarly:
ycm=m1y1+m2y2+m3y3M
Substituting the values:
ycm=(1)(0)+(32)(√32a)+(2)(0)72
Calculating each term:
ycm=0+3√34a+072=3√34a72=3√3a4⋅27=6√3a28=3√3a14
Final Result
Thus, the coordinates of the center of mass are:
(11a14,3√3a14)
Let's place the three masses at the vertices of an equilateral triangle with side length a. We can assign the following coordinates to the vertices:
- Mass m1=1kg at (0,0)
- Mass m2=32kg at (a2,√32a)
- Mass m3=2kg at (a,0)
The total mass M of the system is given by:
M=m1+m2+m3=1+32+2=72kg
The x-coordinate of the center of mass xcm is calculated using the formula:
xcm=m1x1+m2x2+m3x3M
Substituting the values:
xcm=(1)(0)+(32)(a2)+(2)(a)72
Calculating each term:
xcm=0+3a4+2a72=3a4+8a472=11a472=11a4⋅27=22a28=11a14
The y-coordinate of the center of mass ycm is calculated similarly:
ycm=m1y1+m2y2+m3y3M
Substituting the values:
ycm=(1)(0)+(32)(√32a)+(2)(0)72
Calculating each term:
ycm=0+3√34a+072=3√34a72=3√3a4⋅27=6√3a28=3√3a14
Thus, the coordinates of the center of mass are:
(11a14,3√3a14)
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBook:NCERT FINGERTPS ENGLISHChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSExercise:MOTION OF CENTRE OF MASS
Explore 10 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBook:NCERT FINGERTPS ENGLISHChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSExercise:TORQUE AND ANGULAR MOMENTUM
Explore 11 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBook:NCERT FINGERTPS ENGLISHChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSExercise:NCERT Exemplar
Explore 8 Videos
- PRACTICE PAPERSBook:NCERT FINGERTPS ENGLISHChapter:PRACTICE PAPERSExercise:All Questions
Explore 150 Videos
- THERMAL PROPERTIES OF MATTERBook:NCERT FINGERTPS ENGLISHChapter:THERMAL PROPERTIES OF MATTERExercise:Assertion And Reason
Explore 10 Videos
Similar Questions
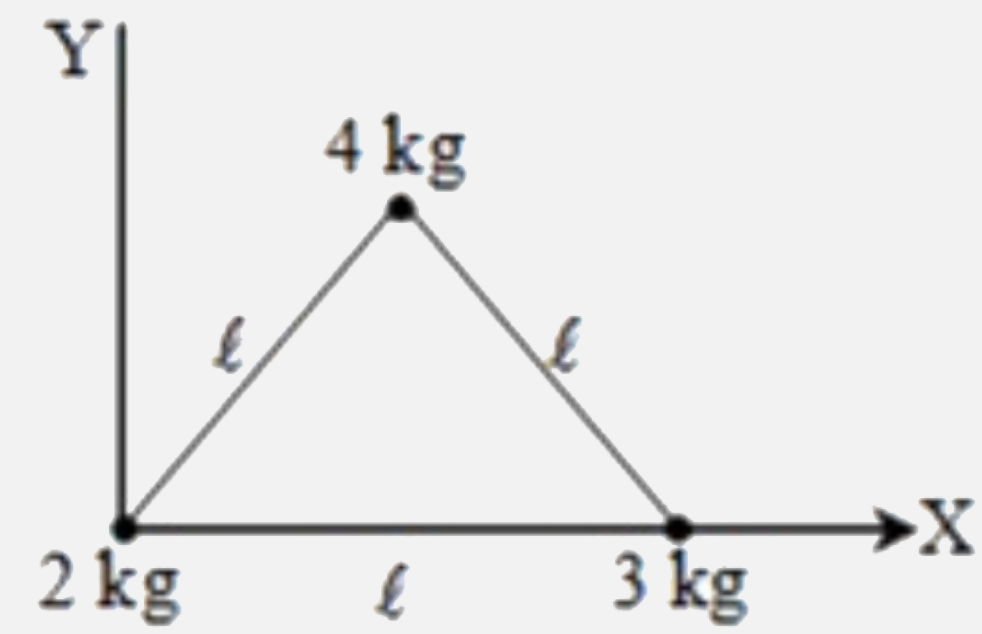
Three masses 2 kg , 3kg and 4kg are lying at the corners of an equilateral triangle of side I. The X coordinate of center of mass is
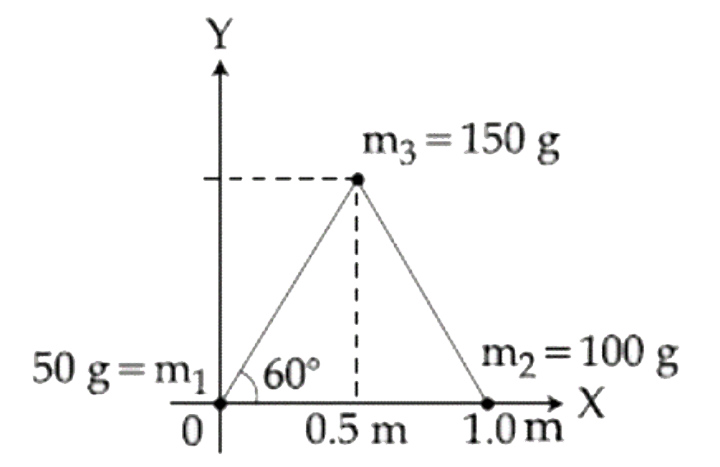
View SolutionThree particles of massses 50 g, 100 g and 150 g are placed at the vertices of an equilateral triangle of side 1m ( as shown in the figure ) . The ( x, y) coordinates of the centre of mass will be :
View SolutionThree particles of masses 1.0 kg 2.0 kg and 3.0 kg are placed at the corners A,B and C respectively of an equilateral triangle ABC of edge 1m. Locate the centre of mass of the system.
View SolutionThe coordinates of a triangle ABC are A(1,2), B(4,6) and C(−3,−2). Three particles of masses 1kg, 2kg and mkg are placed the vertices of the triangle. If the coordinate of the centre of mass are (35,2), calculate the mass m.
View SolutionThree masses of 2 kg, 3 kg and 4 kg are located at the three vertices of an equilateral triangle of side 1 m. What is the M.I. of the system about an axis along the altitude of the triangle and passing through the 3 kg mass?
View SolutionThree balls of masses 1kg,2kgand3kg are arranged at the corners of an equilateral triangle of side 1m. What will be the moment of inertia of the system and perpendicular to the plane of the triangle.
View SolutionThree particles of equal mass 'm' are situated at the vertices of an equilateral triangle of side L. The work done in increasing the side of the triangle to 2L is
View SolutionThree point masses m1,m2 and m3 are located at the vertices of an equilateral triangle of side α. What is the moment of inertia of the system about an axis along the altitude of the triangle passing through m1?
View SolutionThree point masses m1,m2 and m3 are located at the vertices of an equilateral triangle of side α. What is the moment of inertia of the system about an axis along the altitude of the triangle passing through m1?
View SolutionThree particles of masses 1kg, 2kg and 3kg are placed at the corners A, B and C respectively of an equilateral triangle ABC of edge 1m. Find the distance of their centre of mass from A.
View Solution

