Three particles, each of mass m are situated at the vertices of an equilateral triangle ABC of side L as shown in the figure. Find the moment of inertia of the system about the line AX perpendicular to AB in the plane of ABC

Perpendicular distance of A from AX=0
Perpendicular distance B from AX=L
Perpendicular distance of DC from AX=L/2
Thus, the moment of inertia of the particle at A=0, of the particle at B=mL2 and of the particle at C=m(L2)2. The moment of inertia of the three particle system about AX is
0+mL2+m(L2)2=5mL24
Note that the particle on the axis do not contribute to the moment of inertia.
Related Playlists
- BOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - worked out Examples29videos
ROTATIONAL MECHANICS
- BOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective -126videos
ROTATIONAL MECHANICS
- BOOK - HC VERMA ENGLISHCHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Question for short Answer13videos
REST AND MOTION : KINEMATICS
- BOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Question for short Answer15videos
SIMPLE HARMONIC MOTION
Similar Questions
Three particles, each of mass m are situated at the vertices of an equilateral triangle ABC of side l (as shown in the figure).
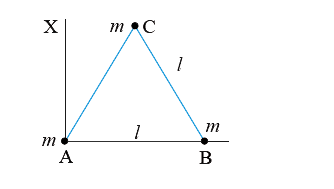
The moment of inertia of the system about a line AX perpendicular to AB and in the plane of ABC, will be:View SolutionThree particles, each of mass m grams situated at the vertices of an equilateral triangle AbC of side I cm (as shown in the figure). The moment of inertia of the system about a line AX perpendicular to AB and in the plane of ABC, in gram-cm^2 units will be.
 .View Solution
.View SolutionFind the coordinates of the vertices of an equilateral triangle of side 2a as shown in Figure.
View SolutionThree particles of equal mass 'm' are situated at the vertices of an equilateral triangle of side L. The work done in increasing the side of the triangle to 2L is
View SolutionThree particle each of mass m are placed at the corners of equilateral triangle of side l

Which of the following is/are correct ?View SolutionThree masses each of mass m are palced at the vertices of an equilateral triangles ABC of side l as shown in figure. The force acting on a mass 2m placed at the centroid O of the triangle is
 View Solution
View Solution
Three rods each of mass m and length l are joined together to form an equilateral triangle as shown in figure. Find the moment of inertial of the system about an axis passing through its centre of mass and perpendicular to the plane of the particle.View Solution
Three rods each of mass m and length l are joined together to form an equilateral triangle as shown in figure. Find the moment of inertial of the system about an axis passing through its centre of mass and perpendicular to the plane of the particle.View SolutionThree particles each of mass m are kept at vertices of an equilateral triangle of side L. The gravitational field at centre due to these particle is
View SolutionThree point masses are arranged as shown in the figure. Moment of inertia of the system about the axis OO' is
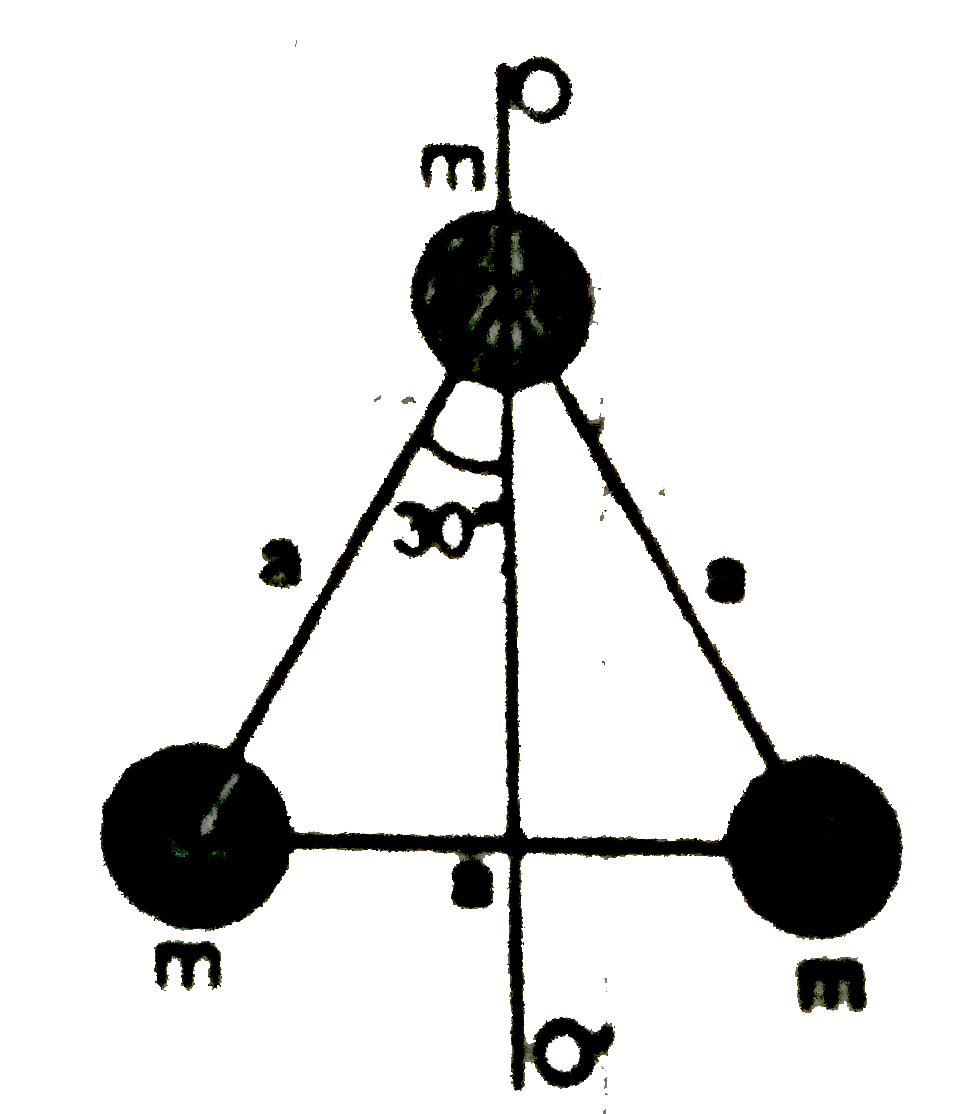 View Solution
View Solution


