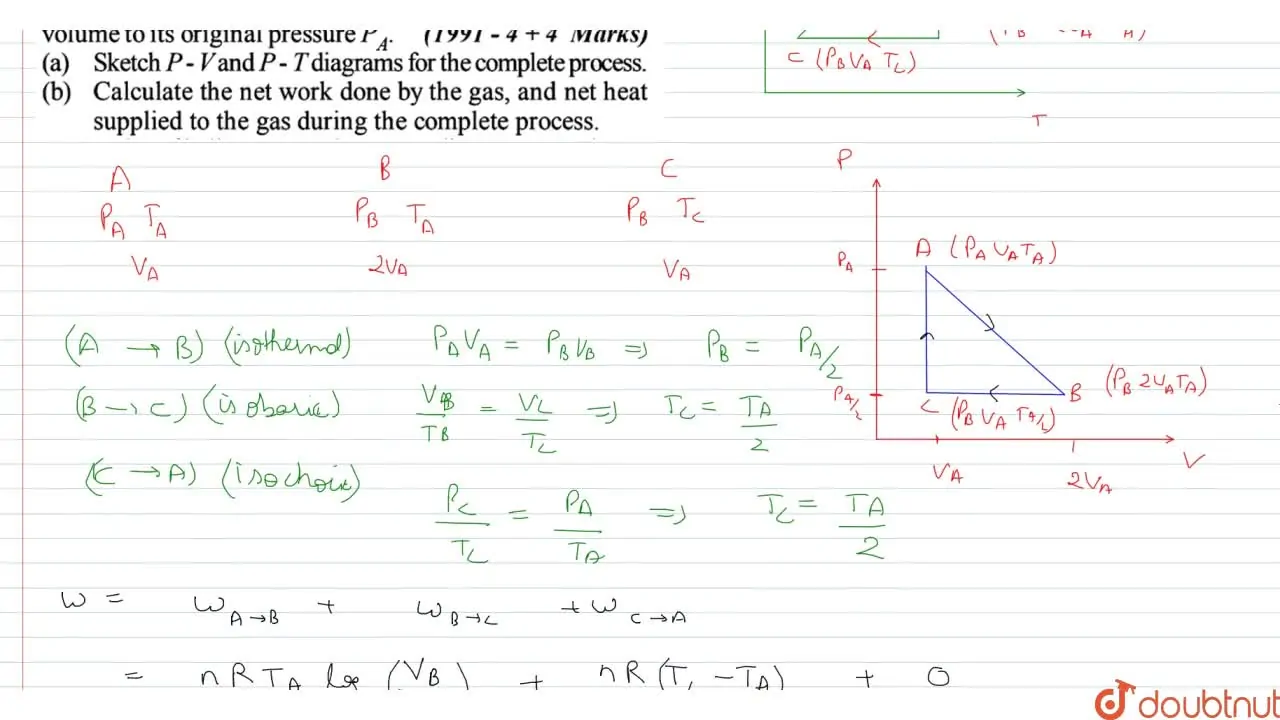
Three moles of an ideal gas (Cp=72R) at pressure, PA and temperature TA is isothermally expanded to twice its initial volume. It is then compressed at constant pressure to its original volume. Finally gas is compressed at constant volume to its original pressure PA.
(a) Sketch P-V and P-T diagrams for the complete process.
(b) Calculate the net work done by the gas, and net heat supplied to the gas during the complete process.
The correct Answer is:B, D
(a) Process A to B (isothermal expansion)
PAVA=PBVB
⇒PAVA=PB2VA
⇒PB=PA2
Process B to C (isobaric
compression)

VBTB=VCTC
⇒2VATA=VATC
⇒TC=TA2
Process C to A [volume is constant]
PCTC=PATA⇒PBTC=PATA
⇒(PA)/2TC=PATA⇒TC=TA2

Let the system initially be at point A at pressure PA and temp
TA and volume VA.
Process A to B
The system is isothermally expanded and reaches a new
state B(PB,2VA,TA) as shown in the figure.
Process B to C
The system is the compressed at constant pressure to its
original volume to reach at state C(PB,VA,TC)
Process C to A
Finally at constant volume, the pressure is increased to its
original pressure to each the state A again.
(b) The total work done
W=WA→B+WB→C+WC→A
=nRTAloge(VB)VA+nR(TC−TA)+0
=2.303×3×R×TAlog10(2VA)VA+3R(TA2−TA)
=2.08RTA−32RTA=0.58RTA
Related Playlists
Similar Questions
Three moles of an ideal gas (Cp=7/2R) at pressure pA and temperature TA is isothermally expanded to twice its initial volume. It is then composed at constant pressure to its original volume. Finally the gas is compressed at constant volume to its original pressure pA (i) Sketch p−V and p−T diagrams for the complete process (b) Calculate the net work done by the gas and net heat supplied to the gas a during the complete process.
View SolutionThree moles of an ideal gas Cp=7/2R at pressure PA and temperature TA is isothermally expanded to twice its initial volume. It is then compressed at constant pressure to its original volume. Finally the gas is compressed at constant volume to the original pressure PA.The correct P-V and P-T diagram indicating the process are
View SolutionThree moles of an ideal gas (Cp=72R) at pressure p0 and temperature T0 is isothermally expanded to twice its initial volume. It is then compressed at a constant pressure to its original volume.
(a) Sketch p-V and p-T diagram for complete process.
(b) Calculate net work done by the gas.
(c) Calculate net heat supplied to the gas during complete process.
(Write your answer in terms of gas constant =R)View SolutionA sample of an ideal gas has pressure p0, volume V0 and tempreture T0. It is isothermally expanded to twice its oringinal volume.it is then compressed at constant pressure to have the original volume V0. Finally, the gas is heated at constant volume to get the original tempreture.(a) show the process in a V-T diagram (b) calculate the heat absorbed in the process.
View SolutionAn ideal gas intially has pressure P volume V and temperature T. Its is isothermally expanded to four times of its original volume, then it is compressed at constant pressure to attain its original volume V. Finally, the gas is heated at constant volume to get the original temperature T. (a) Draw V−T curve (b) Calculate the total work done by the gas in the process.(given ln2=0.693)
View SolutionIf a gas is heated at constant pressure, its isothermal compressibility
View SolutionOne mole of an ideal gas at pressure P0 and temperature T0 is expanded isothermally to twice ist volume and then compressed at constant pressure to (V0/2) and the gas is brought bac to original state by a process in which PαV (pressure is direclty proportional to volume). The correct temperature of the process is
View SolutionA gas is suddenly compressed to one fourth of its original volume. What will be its final pressure, if its initial pressure is p
View SolutionA mass of ideal gas at pressure P is expanded isothermally to four times the original volume and then slowly compressed adiabatically to its original volume. Assuming γ to be 1.5, the new pressure of the gas is
View SolutionOne gram mole of an ideal gas at N.T.P is first expanded isothermally to twice the origional volume. It is then compressed at constant volume, till its pressure is raised to the original value. Calculate the total amount of work done. Given R=8.3mole_1K−1.
View Solution