There is a constant homogeneous electric field of 100Vm−1 within the region x=0andx=0.167m pointing in x-direction. There is a constant homogeneous mangetic field B within the region x=0.167mandx=0.334m pointing in the z-direction. A proton at rest at the origin is released in positive x-direction. Find the minimum strength of the magnetic field B, so that the proton is detected back at x=0,y=0.167m. (mass of proton =1.67×10−27kg)
First of all the proton is accelerated in the electric field.
Then it enters in magnetic field and describes a circular path. After that it leaves the magnetic field and describes a circular path.
After that it leaves the magnetic field in negative direction. Its
motion is retarded in electric field. Finally, it strikes y-axis at
the same distance 0.167m.

Let us first calculate the velocity of the proton when it entres in
magnetic field after traversing in electric field.
Force acting on proton in electric field =eE
∴ Acceleration of proton a=(eEm)
Using the formula v2+u2=2as, we have
v2=2(eEm)s=2(eEm)(0.167)....(i)
Now consider the motion in magnetic field. The proton describes
a circular path of radius (AC/2).
Hence, mv2r=evBorB=mver....(ii)
∴B=me(0.1667/2)×√[2eEm(0.167)]
=2√(2me×E0.167)=2
⎷[2(2.67×10−27)(100)1.6×10−19(0.167)]
=10−2√2=7.07×10−3T
Related Playlists
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercise 1.122videos
MAGNETIC FIELD AND MAGNETIC FORCES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercise 1.213videos
MAGNETIC FIELD AND MAGNETIC FORCES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type2videos
MAGNETIC FIELD AND MAGNETIC FORCES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Concept Based8videos
INDUCTANCE
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False3videos
MISCELLANEOUS VOLUME 3
Similar Questions
A particle of mass 20g experiences a gravitational force of 4.0N along positive x - direction. Find the gravitational field at that point.
View SolutionA proton is moving along Z-axis in a magnetic field. The magnetic field is along X-axis. The proton will experience a force along
View SolutionA current of 10A is established in a long wire along the positive z-axis. Find the magnetic field (vec B) at the point (1m , 0 , 0).
View SolutionA plane electromagnetic wave propagating in the x-direction has wavelength of 6.0mm. The electric field is in the y-direction and its maximum magnitude of 33Vm−1. The equation for the electric field as function of x and l is
View SolutionA uniform electric field is present in the positive x - direction. If the intensity of the field is 5NC−1 then find the potential difference (VB−VA) between two points A (0 m, 2 m) and B (5 m, 3 m).
View SolutionAn electron is moving along +x direction with a velocity of 6×106ms−1 . It enters a region of uniform electric field of 300 V/cm pointing along + y direction. The magnitude and direction of the magnetic field set up in this region such that the electron keeps moving along the x direction will be :
View SolutionThe electric field in a region is radially outward with magnitude E = 2r. The charge contained in a sphere of radius a = 2m centerd at the origin is 4xπε0. Find the value of x.
View SolutionIn a certain region of space a uniform and constant electric field and a magnetic field parallel to each other are present. A proton is fired from a point A in the field with speed V=4×104m/s at an angle of α with the field direction. The proton reaches a point B in the field where its velocity makes an angle β with the field direction. If sinαsinβ=√3. Find the electric potential difference between the points A and B. Take mp (mass of proton) =1.6×10−27kg and e (magnitude of electronic charge) =1.6×10−19C.
View SolutionA graph of the x-component of the electric field as a function of x in a region of space is shown in the figure.
They y and z-components of the electric field are zero in this region. The electric potential at the origin is 10 V.
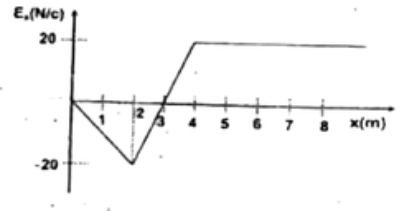
The greatest positive value of electric potential for points of the x-axis for which 0≤x≤6m isView SolutionA charged particle (charge q, mass m) has velocity v0 at origin in +x direction. In space there is a uniform magnetic field B in -z direction. Find the y coordinate of particle when is crosses y axis.
View Solution


