The time period of a physical pendulum about some pivot point is T. When we take another pivot point, opposite of the first one such that the centre of mass of the physical pendulum lies on the line joining these two pivot points, we obtain the same time period. If the two points are separated by a distance L, then the time period T is
2π√Lg
π√Lg
2π√L2g
π√2Lg
The correct Answer is:A
Step by step video & image solution for The time period of a physical pendulum about some pivot point is T. When we take another pivot point, opposite of the first one such that the centre of mass of the physical pendulum lies on the line joining these two pivot points, we obtain the same time period. If the two points are separated by a distance L, then the time period T is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
The temperature of a physical pendulum, whose time period is T, is raised by Δθ. The change in its time period is
View SolutionThe ability to move from one point to another in the shortest period of time:
View SolutionA body of mass m has time period T1 with one spring and has time period T2 with another spring. If both the springs are connected in parallel and same mass is used, then new time period T is given as
View Solution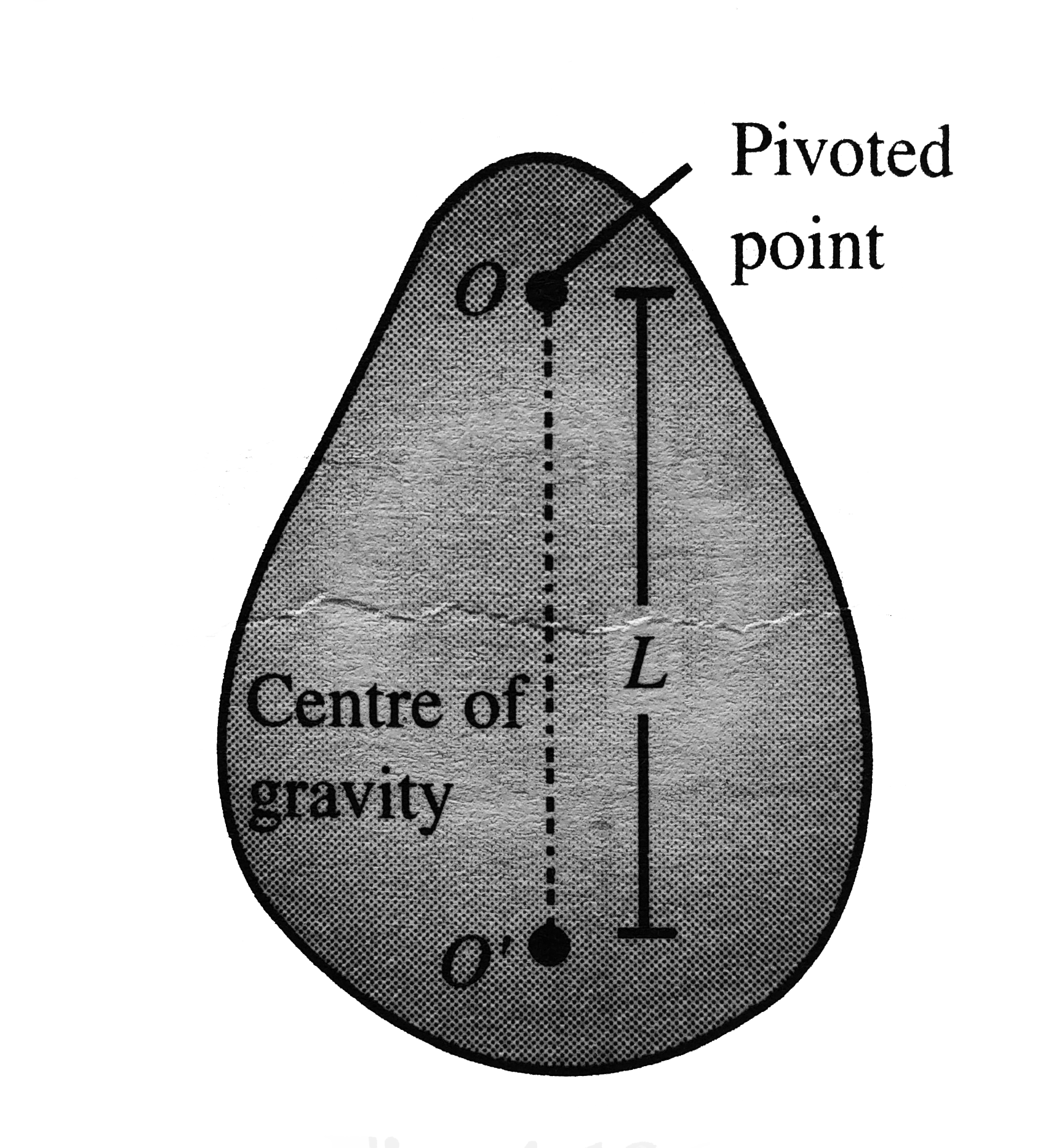
In physical pendulum, the time period for small oscillation is given by T=2π√IMgd where I is the moment of inertial of the body about an axis passing through a pivoted point O and perpendicular to the plane of oscillation and d is the separation point between centre of gravity and the pivoted point. In the physical pendulum a speacial point exists where if we concentrate the entire mass of body, the resulting simple pendulum (w.r.t. pivot point O) will have the same time period as that of physical pendulum This point is termed centre of oscillation.
T=2π√IMgd=2π√Lg Moreover, this point possesses two other important remarkable properties:
Property I: Time period of physical pendulum about the centre of oscillation (if it would be pivoted) is same as in the original case.
Property II: If an impulse is applied at the centre of oscillatioin in the plane of oscillation, the effect of this impulse at pivoted point is zero. Because of this property, this point is also known as the centre of percussion. From the given information answer the following question:
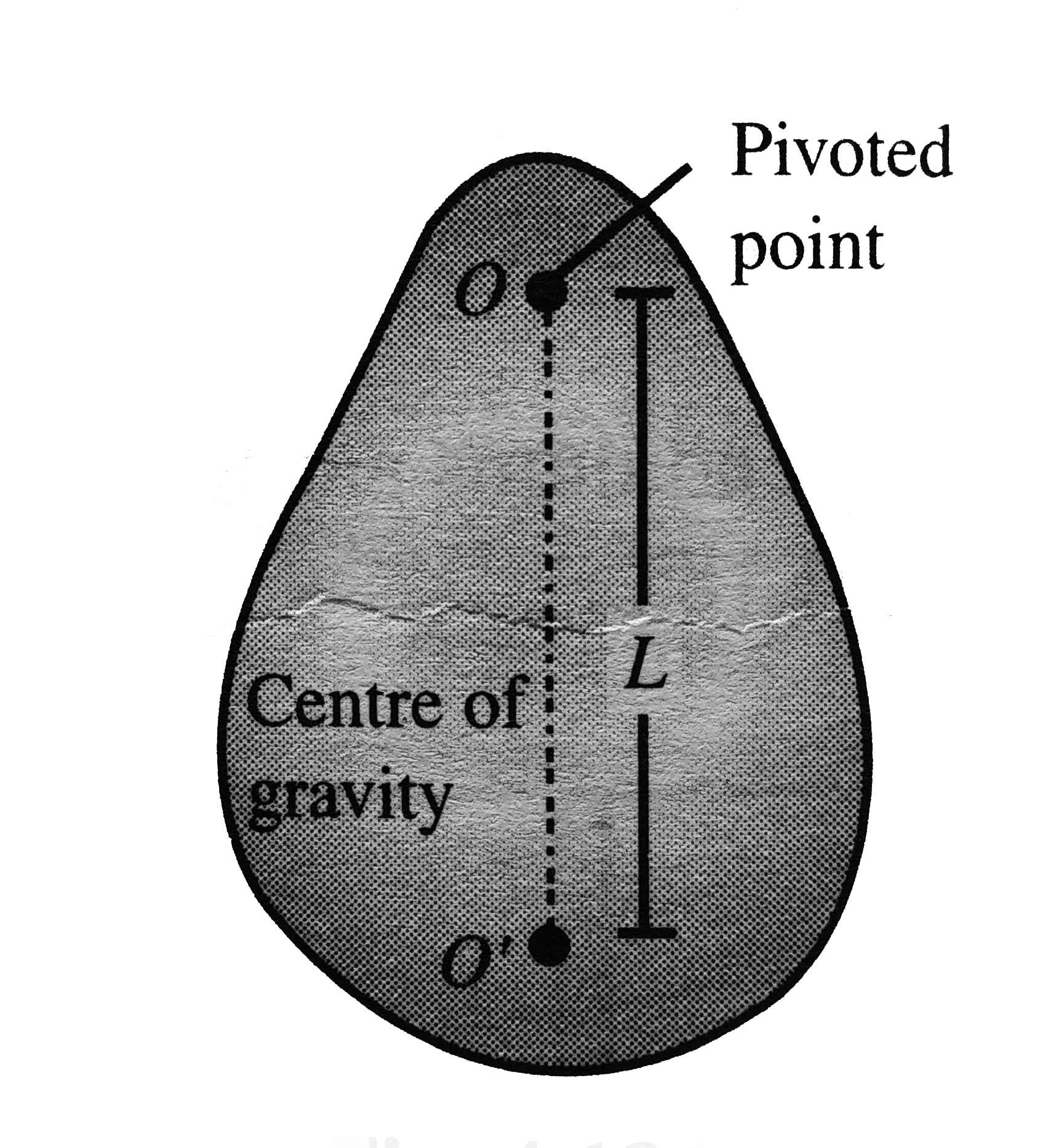
Q. A uniform rod of mass M and length L is pivoted about point O as shown in Figgt It is slightly rotated from its mean position so that it performs angular simple harmonic motion. For this physical pendulum, determine the time period oscillation.View SolutionIn physical pendulum, the time period for small oscillation is given by T=2π√IMgd where I is the moment of inertial of the body about an axis passing through a pivoted point O and perpendicular to the plane of oscillation and d is the separation point between centre of gravity and the pivoted point. In the physical pendulum a speacial point exists where if we concentrate the entire mass of body, the resulting simple pendulum (w.r.t. pivot point O) will have the same time period as that of physical pendulum This point is termed centre of oscillation.
T=2π√IMgd=2π√Lg Moreover, this point possesses two other important remarkable properties:
Property I: Time period of physical pendulum about the centre of oscillation (if it would be pivoted) is same as in the original case.
Property II: If an impulse is applied at the centre of oscillatioin in the plane of oscillation, the effect of this impulse at pivoted point is zero. Because of this property, this point is also known as the centre of percussion. From the given information answer the following question:
Q. If an impulse J is applied at the centre of oscillation in the plane of oscillation, then angular velocity of the rod will be .
 View Solution
View SolutionThe distance between the point of suspension and the centre of gravity of a compound pendulum is l and the radius of gyration about the horizontal axis through the centre of gravity is k, then its time period will be
View SolutionThe time period of a bar pendulum when suspended at distance 30cm and 50cm from its centre of gravity comes out to be the same. If the mass of the body is 2kg. Find out its moment of inertia about an axis passing through first point.
_S01_024_Q01.png) View Solution
View SolutionA curve having the condition that the slope of the tangent at some point is two times the slope of the straight line joining the same point to the origin of coordinates is a/an
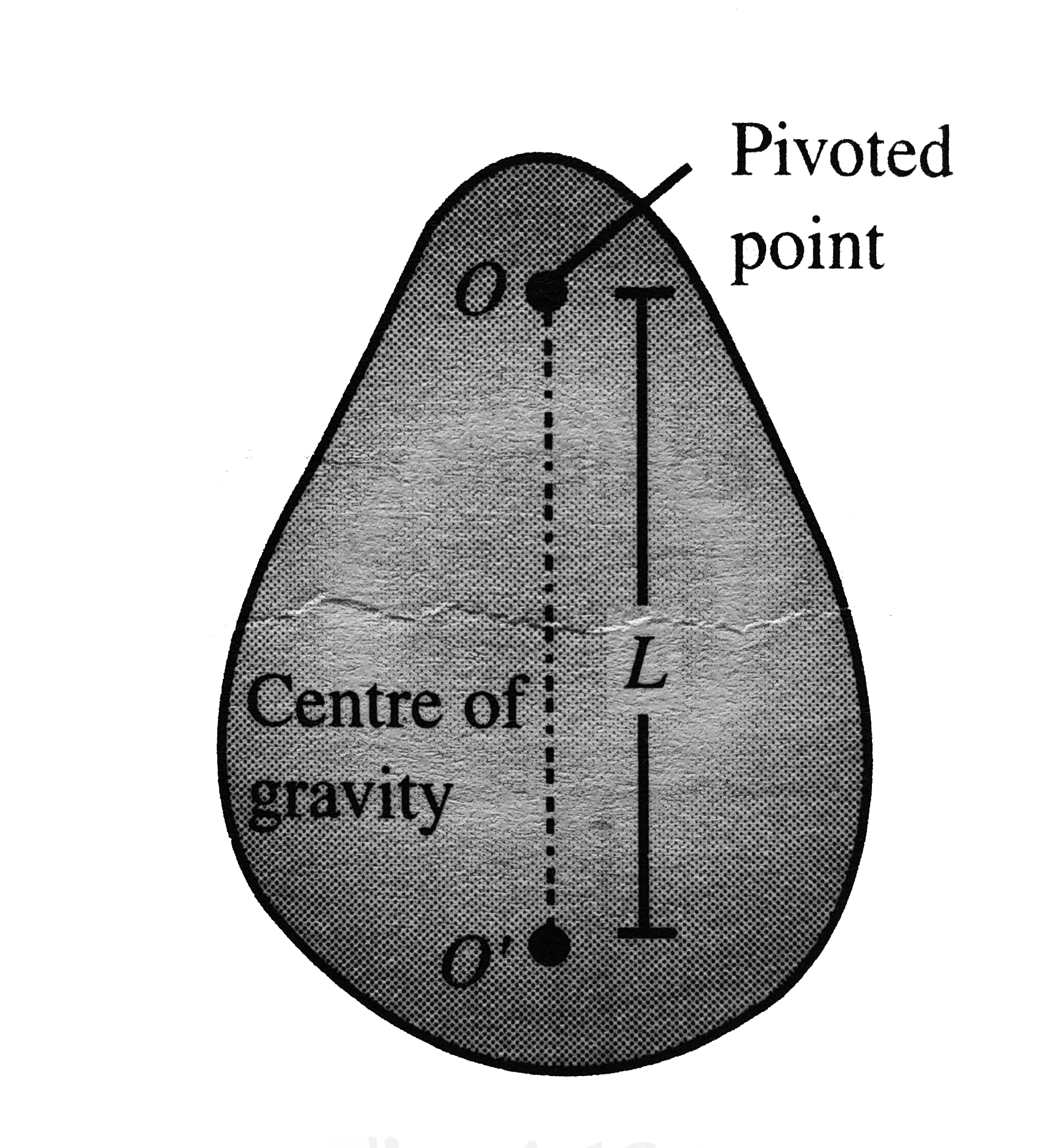
View SolutionIn physical pendulum, the time period for small oscillation is given by T=2π√IMgd where I is the moment of inertial of the body about an axis passing through a pivoted point O and perpendicular to the plane of oscillation and d is the separation point between centre of gravity and the pivoted point. In the physical pendulum a speacial point exists where if we concentrate the entire mass of body, the resulting simple pendulum (w.r.t. pivot point O) will have the same time period as that of physical pendulum This point is termed centre of oscillation.
T=2π√IMgd=2π√Lg Moreover, this point possesses two other important remarkable properties:
Property I: Time period of physical pendulum about the centre of oscillation (if it would be pivoted) is same as in the original case.
Property II: If an impulse is applied at the centre of oscillatioin in the plane of oscillation, the effect of this impulse at pivoted point is zero. Because of this property, this point is also known as the centre of percussion. From the given information answer the following question:
Q. For the above question, locate the centre of oscillation.
 View Solution
View SolutionA uniform circular disc of mass M and radius R is pivoted at distance x above the centre of mass of the disc, such that the time period of the disc in the vertical plane is infinite. What is the distance between the pivoted point and centre of mass of the disc ?
View Solution


