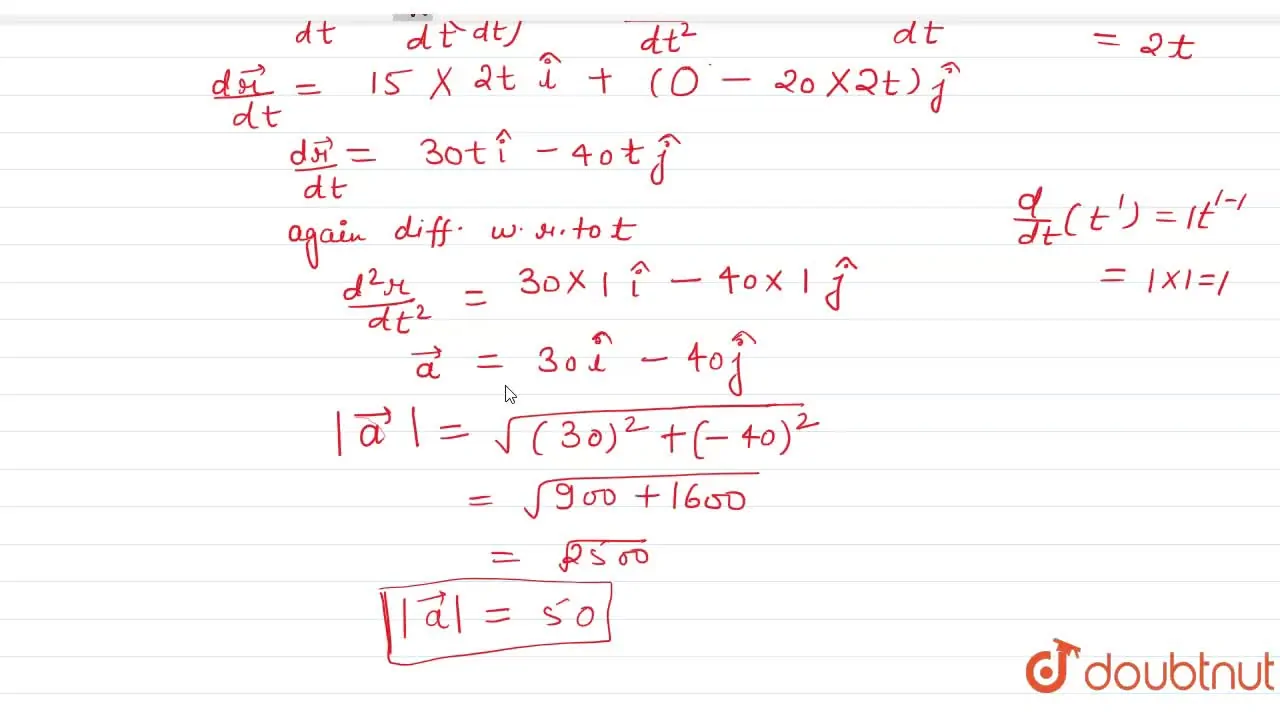The position vector of a particle changes with time according to the relation →r(t)=15t2ˆi+(4−20t2)ˆj What is the magnitude of the acceleration at t = 1?
The correct Answer is:50
→r=15t2ˆi+(4−20t2)ˆj
−→dt2dt2=30ˆi+(−40)ˆj,a=50m/sec2
Similar Questions
The position vector of a partcle →r(t)=15t2ˆi+(4−20t2)ˆj. What is the magnitude of the acceleration (in m/s2) at t=1?
View SolutionIf the position vector of a particle is given by →r=(cos2t)ˆi+(sin2t)ˆj+6tˆkm. Calculate magnitude of its acceleration (in m/s2 ) at t=π4
View SolutionPosition vector →r of a particle varies with time t accordin to the law →r=(12t2)ˆi−(43t1.5)ˆj+(2t)ˆk, where r is in meters and t is in seconds.
(a) Find suitable expression for its velocity and acceleration as function of time (b) Find magnitude of its displacement and distance traveled in the time interval t=0 to 4s.View SolutionThe position vector →r of a moving particle at time t after the start of the motion is given by →r=(5+20t)ˆi+(95+10t−5t2)ˆj. At the t = T, the particle is moving at right angles to its initial direction of motion. Find the value of T and the distance of the particle from its initial position at this time.
View Solution→r=15t2i+(20−20t2)j
find magnitude of acceleration at t=1 sec.View SolutionA particle moves in the xy plane according to the equation
→r=(ˆi+2ˆj)Acosωt
The motion of the particle isView SolutionThe position vector of a particle is determined by the expression →r=3t2ˆi+4t2ˆj+7ˆk. The displacement travelled in first 10 seconds is :
View SolutionThe position of a particle is given by →r=3tˆi−4t2ˆj+5ˆk. Then the magnitude of the velocity of the particle at t = 2 s is
View SolutionA particle moves in x-y plane according to the equation ¯r=(ˆi+2ˆj)Acosωt the motion of the particle is
View SolutionA particle moves in x-y plane according to the equation ¯r=(ˆi+2ˆj)Acosωt. The motion of the particle is
View Solution