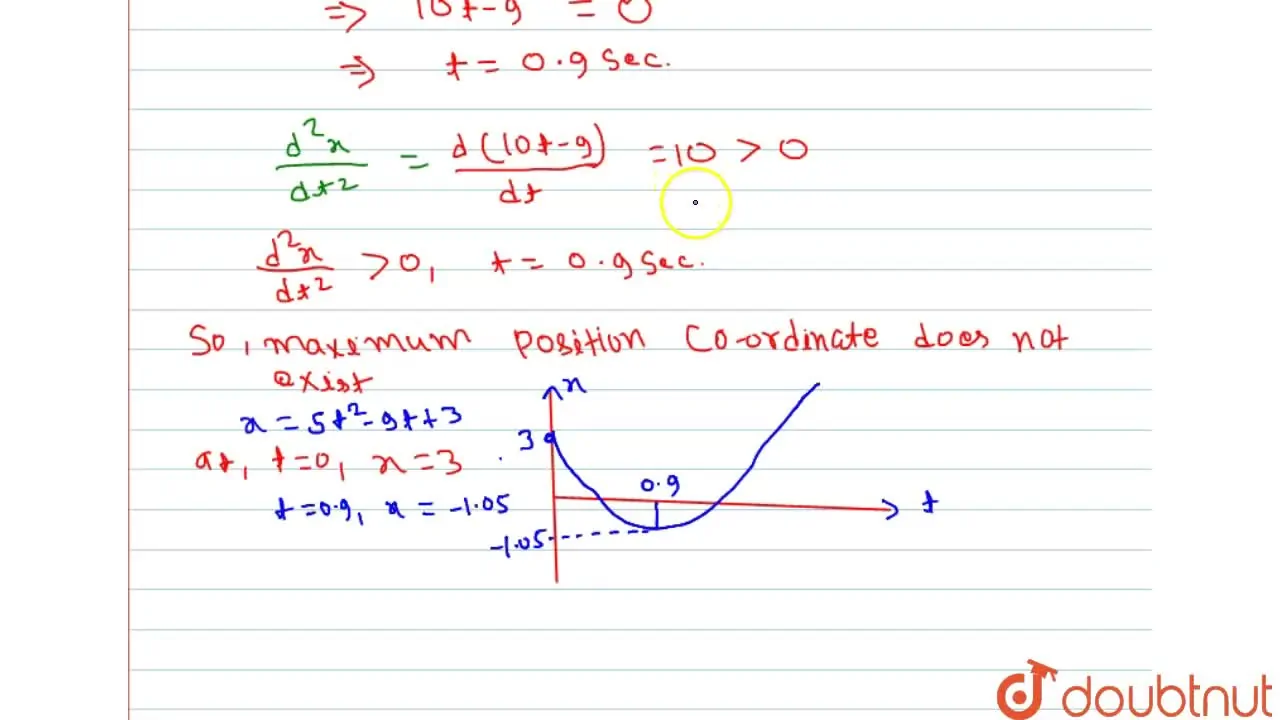
The particle's position as a funciton of time is given as x=5t2−9t+3. Find out the maximum value of position co-ordinate? Also, plot the graph.
We are given x=5t2−9t+3, the position is changing with x.
Differentiate x w.r.t t, we get dxdt=10t−9=0
∴t=9/10=0.9
Check whether maxima or minima exists.
We need to do double differentiation test: d2xdt2=10>0
Therefore, there exists a minima at t=0.9
Now, check for the limiting values.
When t=0, x=3 and when t=∞, x=∞.
So, the maximum position co-ordinate does not exist.
Related Playlists
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - BASIC MATHEMATICSEXERCISE - Solved Examples9videos
BASIC MATHEMATICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise 2.12videos
BASIC MATHEMATICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ARCHIVES 2 VOLUME 6EXERCISE - Integer4videos
ARCHIVES 2 VOLUME 6
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example13videos
CALORIMETRY
Similar Questions
The position of a particle is given by
x=2(t−t2)
where t is expressed in seconds and x is in metre.
The maximum value of position co-ordinate of particle on positive x-axis isView SolutionThe position of a particle is given by x=7+3t3 m and y=13+5t−9t2m, where x and y are the position coordinates, and t is the time in s. Find the speed (magnitude of the velocity) when the x component of the acceleration is 36m/s2.
View SolutionA particle moves along x-axis such that its position veries with time as x=50t−5t2. Select the correct alternative (s).
View SolutionPosition of particle moving along x-axis is given as x=2+5t+7t2 then calculate :
View SolutionFind out the position of particle as a function of time which is moving in a straight line with an acceleration a=5x, where x is position.
(i) At t=0 the particle is at x=0 (ii) Mass of the object is 5kgView SolutionA particle moves along a straight line and its position as a function of time is given by x=t6(3)−3t6(2)+3t+3, then particle
View SolutionIf the velocity of a particle moving along x-axis is given as v=(3t2−2t) and t=0, x=0 then calculate position of the particle at t=2sec.
View SolutionThe position of a particle moving along x-axis varies eith time t as x=4t−t2+1. Find the time interval(s) during which the particle is moving along positive x-direction.
View SolutionThe acceleration of a particle varies with time t seconds according to the relation a=6t+6ms−2. Find velocity and position as funcitons of time. It is given that the particle starts from origin at t=0 with velocity 2ms−1.
View SolutionVelocity of a particle in x-y plane at any time t is v=(2tˆi+3t2ˆj)m/s At t=0, particle starts from the co-ordinates (2m,4m). Find
(a) acceleration of the particle at t=1s.
(b) position vector and co-ordinates of the particle at t=2s.View Solution