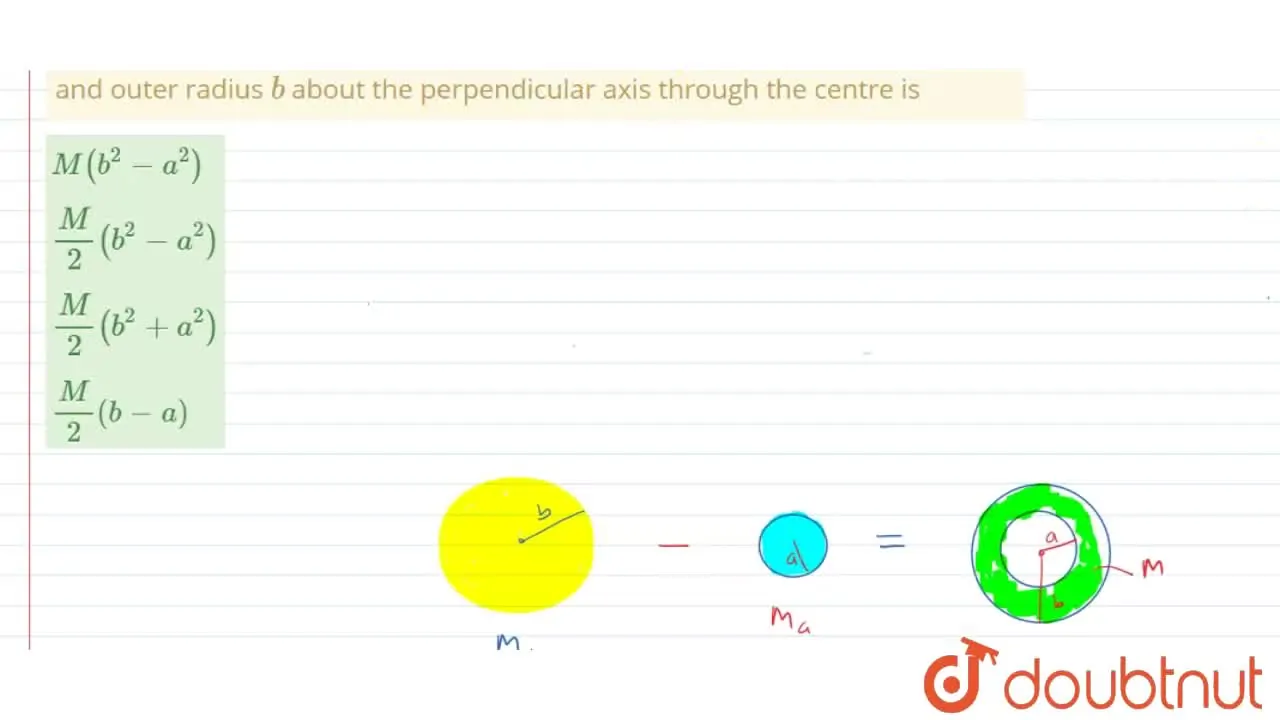
The moment of inertia of a flat angular ring is having mass M, inner radius a and outer radius b about the perpendicular axis through the centre is
M(b2−a2)
M2(b2−a2)
M2(b2+a2)
M2(b−a)
Step by step video & image solution for The moment of inertia of a flat angular ring is having mass M, inner radius a and outer radius b about the perpendicular axis through the centre is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - C) Objective Type Questions (More than one option are correct)29videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - D) Linked Comprehension Type Questions20videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - A) Objective Type Questions (One option is correct)62videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - Assignment (Section-D (Assertion and reason))5videos
SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TEST 1EXERCISE - EXERCISE21videos
TEST 1
Similar Questions
The moment of inertia of a flat annular ring having mass M, inner radius a and outer radius b about the diametric axis through the centre is
View SolutionThe moment of inertia of a uniform semicircular disc of mass M and radius r about a line perpendicular to the plane of the disc through the center is
View SolutionThe moment of inertia of a uniform semicircularwire of mass M and radius r about a line perpendicular to the plane of the wire through the centre is :
View SolutionCalculate the moment of inertia of a ring having mass M, radius Rand having uniform mass distribution about an axis passing through the centre of the ring and perpendicular to the plane of the ring?
 View Solution
View Solution
Calculate the moments of inertia of the figures shown, each having mass M, radius R and having uniform mass distribution about an axis perpendicular to the plane and passing through the centre?View SolutionThe moment of inertia of a uniform semicircular wire of mass 'M' and radius 'r' about a line perpendicular to the plane of the wire through the center is
View SolutionFind the moment of inertia of a uniform ring of mass M and radius R about a diameter.
View SolutionFind out the moment of inertia of the circular arcs shown, each having mass M, radius R and having uniform mass distribution about an axis passing through the centre and perpendicular to the plane ?
 View Solution
View SolutionThe moment of inertia of a hoop of radius R and mass M, about any tangent
View SolutionMoment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
View Solution