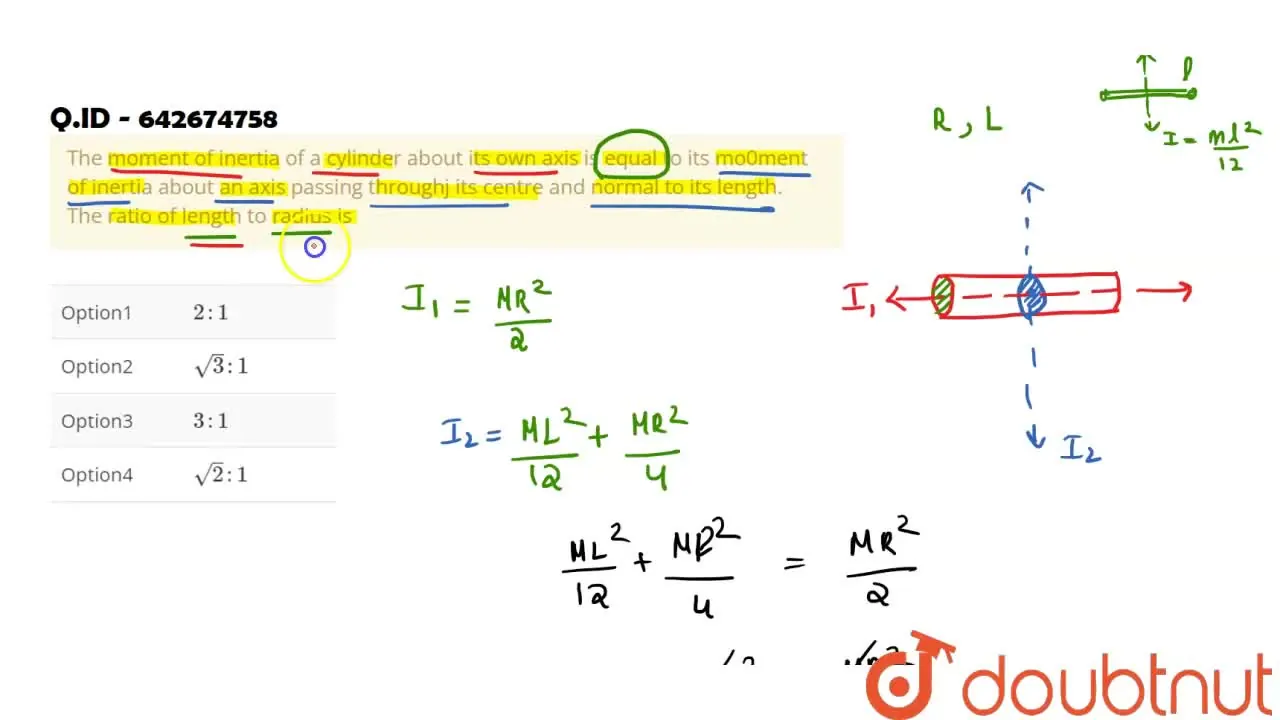
The moment of inertia of a cylinder about its own axis is equal to its mo0ment of inertia about an axis passing throughj its centre and normal to its length. The ratio of length to radius is Solution in Telugu
2:1
√3:1
3:1
√2:1
The correct Answer is:B
Step by step video, text & image solution for The moment of inertia of a cylinder about its own axis is equal to its mo0ment of inertia about an axis passing throughj its centre and normal to its length. The ratio of length to radius is by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Related Playlists
- BOOK - AAKASH SERIESCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - PRACTICE EXERCISE99videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - AAKASH SERIESCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Exercise-I143videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - AAKASH SERIESCHAPTER - SURFACE TENSIONEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS )8videos
SURFACE TENSION
- BOOK - AAKASH SERIESCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II) PRACTICE SHEET (ADVANCED) Integer/Subjective Type Questions2videos
THERMAL PROPERTIES OF MATTER
Similar Questions
The centre of mass of two particles with masses 2kg and 6 kg located at (1,1,1), (2,2,1) respectively has the coordinates
02:27View SolutionThree identical spheres each of radius R are placed touching each other on a horizontal table. The centre of mass of the system is located
02:23View SolutionIf the work done in blowing a soap bubble of volume 'V' is W, then the work done in blowing a soap bubble of volume '2V' is
07:20View SolutionA constant pressure gas thermometer has a volume of 200cc, 273.2cc and 525 .1cc at 0°C, 100°C and boiling point of sulphur respectively. The resistance possessed by a platinum wire at the same temperatures as above are 2.000Ω,2.778Ωand5.280Ω respectively. Estimate the boiling point of sulphur on the basis of the two sets of observations.
View SolutionA uniform cylinder has radius R and length L. If the moment of inertia of this cylinder about an axis passing through its centre and normal to its circular face is mg equal to the moment of inertia of the same cylinder about an axis passing through its centre and normal to its length, then
01:18View SolutionMoment of inertia of a disc about its own axis is I. Its moment of inertia about a tangential axis in its plane is
View SolutionA solid cylinder has mass M radius R and length / its moment of inertia about an axis passing through its centre and perpendicular to its own axis is
03:44View SolutionA solid cylinder has mass M radius R and length / its moment of inertia about an axis passing through its centre and perpendicular to its own axis is
03:38View SolutionA cylinder of 500 g and radius 10 cm has moment of inertia about an axis passing through its centre and parallel to its length is
View SolutionThe moment of inertia of a cylinder of radius R, length L and mass M about an axis passing through its centre of mass and normal to its length is
04:10View SolutionThe moment of inertia of a solid cylinder about its own axis is the same as its moment of inertia about an axis passing through its centre of gravity and perpendicular to its length. The relation between its length L and radius R is :
View SolutionThe relation between length L and radius R of the cylinder , if its moment of inertia about its axis is equal to that about the equatorial axis, will be
02:23View SolutionThe moment f inertia of a solid cylinder about an axis parallel to its length and passing through its centre is equal to its moment of inertia about an axis perpendicular to the length of cylinder and passing through its centre . The ratio of radius of cylinder and its length is
View SolutionThe moment of inertia of a cylinder about its own axis is equal to its mo0ment of inertia about an axis passing throughj its centre and normal to its length. The ratio of length to radius is
View SolutionThe moment of inertia of a cylinder about its own axis is equal to its moment of inertia about an axis passing through its centre and normal to its length. The ratio of length to radius is
04:14View Solution