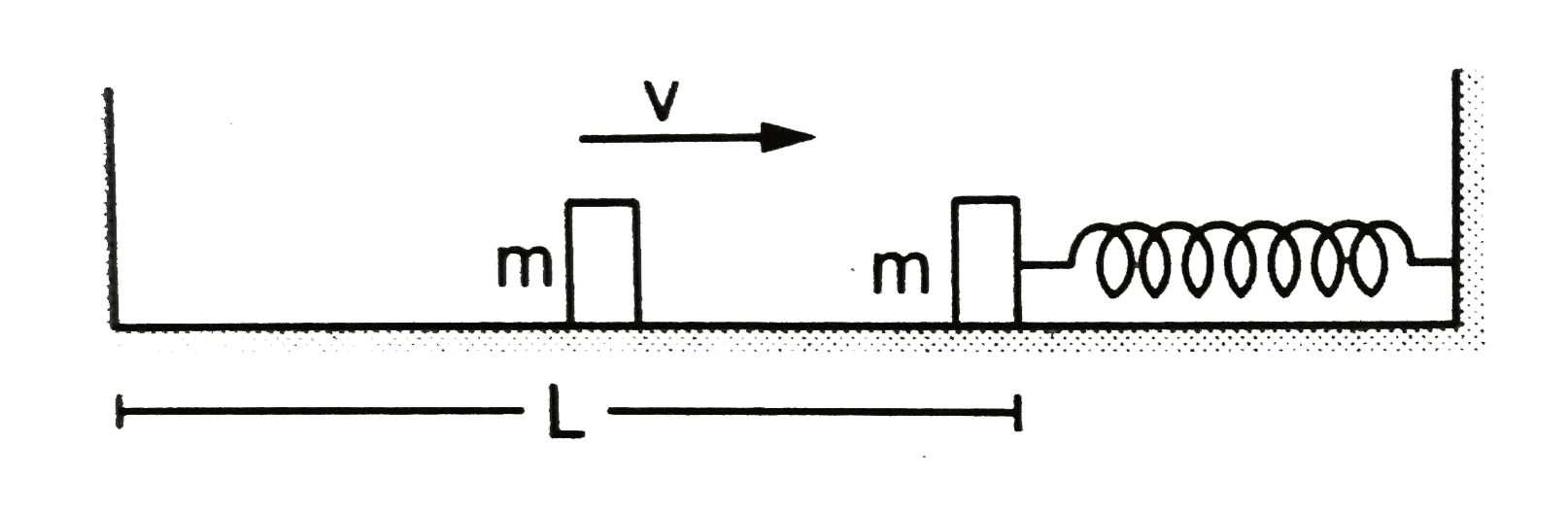
The left block in filgure collides inelastically with the right block and sticks to it. Find the amplitude of the resulting simple harmonic motion.
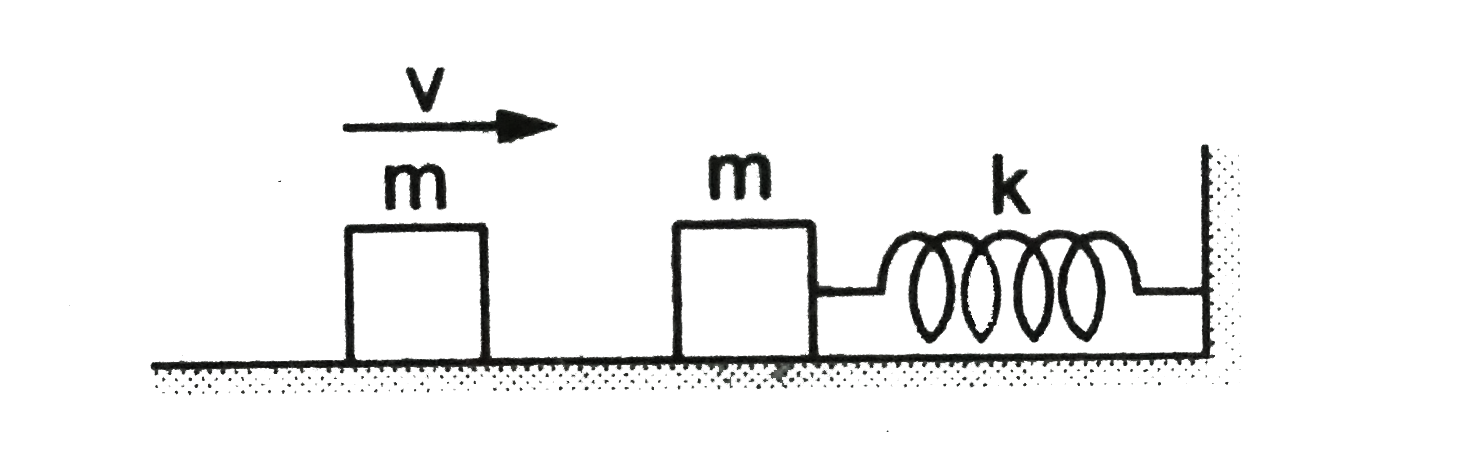
Assuming the collision to last for a small interval only, we can apply the principle of conservationn of momentum. The common velocity after the collisionn is v2. The kinetic energy =12(2m)(v2)2=14mv2. This is also the total energy of vibration as the spring is unstretched at this moment. If the amplitude is A, the total energy can also be written as 12kA2. Thus
=12kA2=14mv2,giv∈gA=√m2kv.
Related Playlists
- BOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Objective -121videos
SIMPLE HARMONIC MOTION
- BOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Objective-215videos
SIMPLE HARMONIC MOTION
- BOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Question for short Answer15videos
SIMPLE HARMONIC MOTION
- BOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for short Answer21videos
ROTATIONAL MECHANICS
- BOOK - HC VERMA ENGLISHCHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Objective-27videos
SOME MECHANICAL PROPERTIES OF MATTER
Similar Questions
In figure, k=100N/m,M=1kg and F=10N

(a) Find the compression of the spring in the equilibrium position
(b) A sharp blow by some external agent imparts a speed of 2m/s to the block towards left. Find the sum of the potential energy of the spring and the kinetic energy of the block at this instant.
(c) Find the time period of the resulting simple harmonic motion.
(d) Find the amplitude.
(e) Write the potential energy of the spring when the block is at the left estreme.
(f) Write the potential energy of the spring when the block is at the right extreme.
The answers of (b), (e) and (f) are different. Explain why this does not violate the principle of conservation of energy ?View SolutionIn the figure shown, the block A of mass m collides with the identical block B and after collision they stick together. Calculate the amplitude of resulatant vibration.
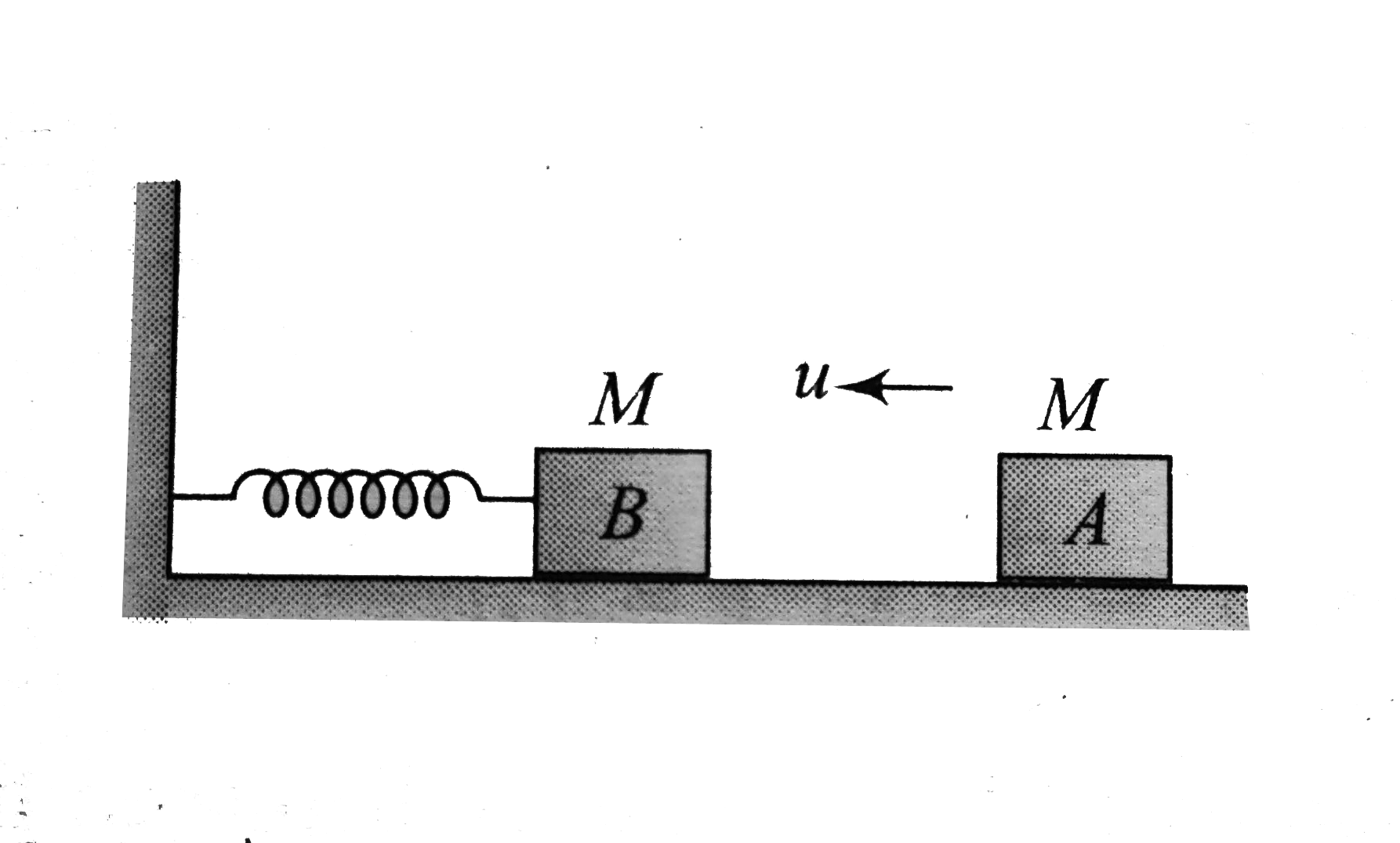 View Solution
View SolutionIn the figure shown, the block A of mass m collides with the identical block B and after collision they stick together. Calculate the amplitude of resulatant vibration.
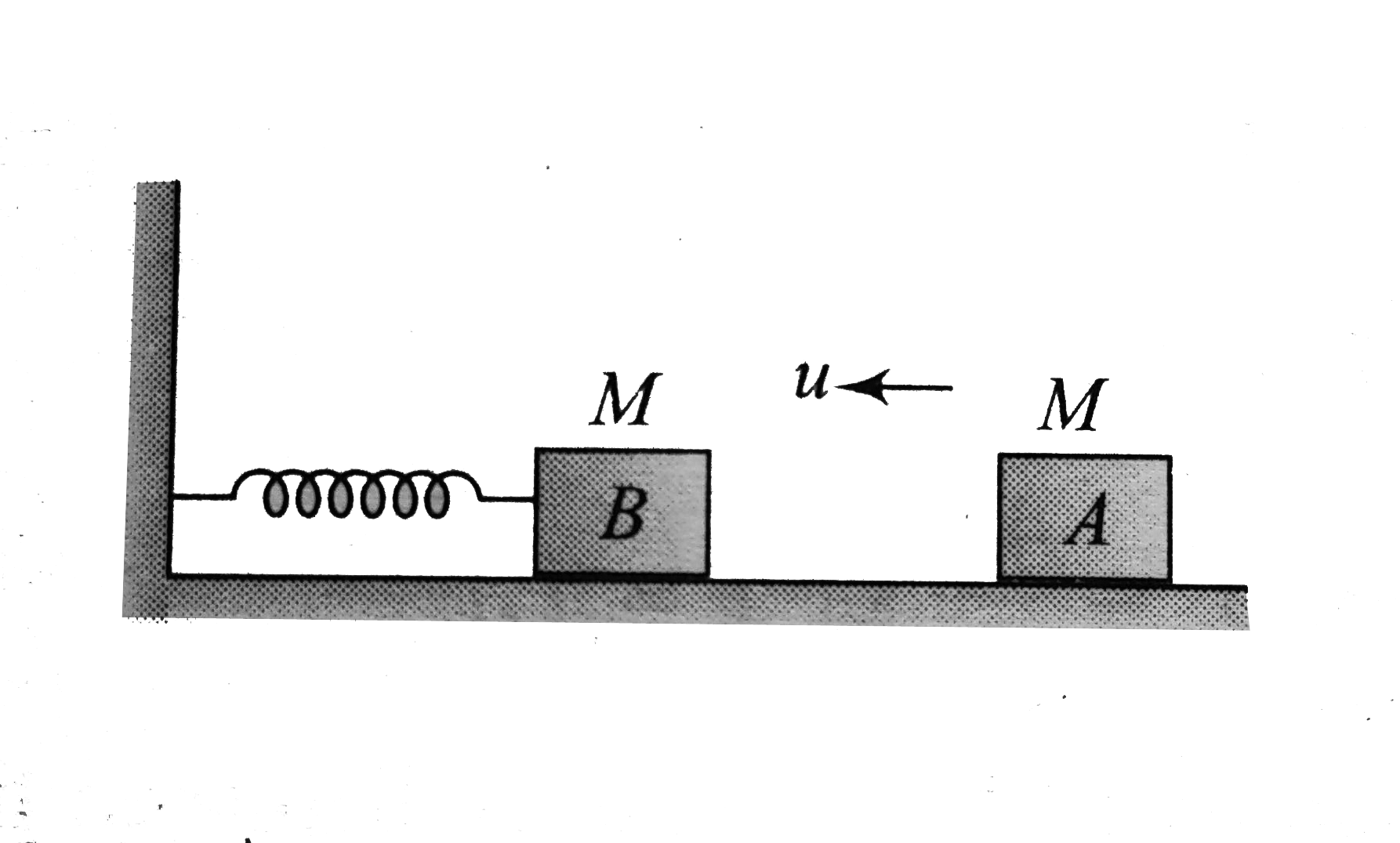 View Solution
View SolutionA bullet of mass m strikes a block of mass M. The bullet remains embedded in the block. Find the amplitude of the resulting SHM.
 View Solution
View SolutionA particle executing of a simple harmonic motion covers a distance equal to half its amplitude in on e second . Then the time period of the simple harmonic motion is
View SolutionThe mass M shown in figure ocillates in simple harmonic motion with amplitude A.
The amplitude of the point P is
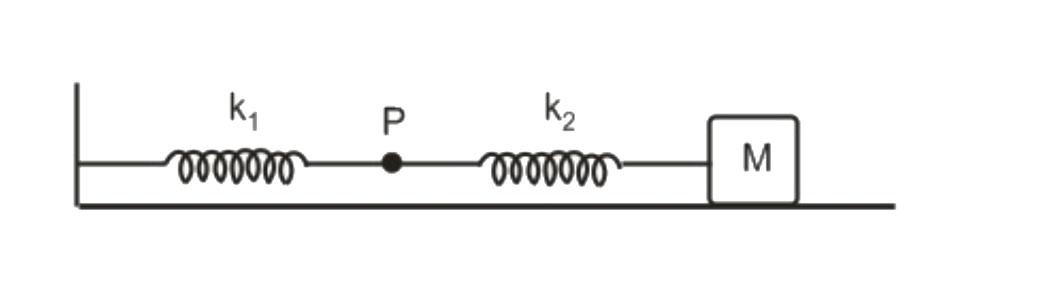 View Solution
View SolutionThe amplitude of given simple harmonic motion is y=(3sinωt+4cosωt)m
View SolutionA block with mass M attached to a horizontal spring with force constant k is moving with simple harmonic motion having amplitude A1. At the instant when the block passes through its equilibrium position a lump of putty with mass m is dropped vertically on the block from a very small height and sticks to it.
(a) Find the new amplitude and period.
(b) Repeat part (a) for the case in which the putty is dropped on the block when it is at one end of its path.View SolutionA block with mass M attached to a horizontal spring with force constant k is moving with simple harmonic motion having amplitude A1. At the instant when the block passes through its equilibrium position a lump of putty with mass m is dropped vertically on the block from a very small height and sticks to it.
(a) Find the new amplitude and period.
(b) Repeat part (a) for the case in which the putty is dropped on the block when it is at one end of its path.View SolutionThe left block in figure moves at a speed v towards the right block placed in equilibrium. All collisions to take place are elastic and the surfaces are frictionless. Show that motion of the two blocks are periodic. Find the time period of these periodic motions. Neglect the widths of the blocks.
 View Solution
View Solution


