The intial velocity of a particle moving along x axis is u (at t = 0 and x = 0) and its acceleration a is given by a = kx. Which of the following equation is correct between its velocity (v) and position (x)?
v2=y2=2kx
v2=u2+2kx2
v2=u2+kx2
v2+u2=2kx
The correct Answer is:C
To solve the problem, we need to derive the relationship between the velocity v and the position x of a particle moving along the x-axis, given that its acceleration a is proportional to its position x (i.e., a=kx).
1. Understand the relationship between acceleration, velocity, and position:
We know that acceleration a can be expressed as:
a=dvdt
Additionally, we can express a in terms of velocity and position using the chain rule:
a=vdvdx
2. Set up the equation:
Given that a=kx, we can equate the two expressions for acceleration:
vdvdx=kx
3. Rearrange the equation:
We can rearrange this equation to separate variables:
vdv=kxdx
4. Integrate both sides:
Now, we integrate both sides. The left side integrates with respect to v and the right side with respect to x:
∫vdv=∫kxdx
This gives us:
v22=kx22+C
where C is the constant of integration.
5. Apply the initial conditions:
We know from the problem that at t=0 and x=0, the initial velocity v=u. We can use this to find C:
u22=k(0)22+C
This simplifies to:
C=u22
6. Substitute back to find the relationship:
Now substituting C back into our integrated equation, we have:
v22=kx22+u22
Multiplying through by 2 to eliminate the fractions gives us:
v2=u2+kx2
Final Result:
The correct equation relating velocity v and position x is:
v2=u2+kx2
We know that acceleration a can be expressed as:
a=dvdt
Additionally, we can express a in terms of velocity and position using the chain rule:
a=vdvdx
Given that a=kx, we can equate the two expressions for acceleration:
vdvdx=kx
We can rearrange this equation to separate variables:
vdv=kxdx
Now, we integrate both sides. The left side integrates with respect to v and the right side with respect to x:
∫vdv=∫kxdx
This gives us:
v22=kx22+C
where C is the constant of integration.
We know from the problem that at t=0 and x=0, the initial velocity v=u. We can use this to find C:
u22=k(0)22+C
This simplifies to:
C=u22
Now substituting C back into our integrated equation, we have:
v22=kx22+u22
Multiplying through by 2 to eliminate the fractions gives us:
v2=u2+kx2
The correct equation relating velocity v and position x is:
v2=u2+kx2
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBook:AAKASH INSTITUTE ENGLISHChapter:MOTION IN A STRAIGHT LINEExercise:ASSIGNMENT (SECTION - C)
Explore 36 Videos
- MOTION IN A STRAIGHT LINEBook:AAKASH INSTITUTE ENGLISHChapter:MOTION IN A STRAIGHT LINEExercise:ASSIGNMENT (SECTION - D)
Explore 15 Videos
- MOTION IN A STRAIGHT LINEBook:AAKASH INSTITUTE ENGLISHChapter:MOTION IN A STRAIGHT LINEExercise:ASSIGNMENT (SECTION - A)
Explore 58 Videos
- MOTION IN A PLANEBook:AAKASH INSTITUTE ENGLISHChapter:MOTION IN A PLANEExercise:Assignement section -J (Aakash Challengers Questions)
Explore 7 Videos
- MOTION IN STRAIGHT LINEBook:AAKASH INSTITUTE ENGLISHChapter:MOTION IN STRAIGHT LINEExercise:Assignment (SECTION - J)
Explore 2 Videos
Similar Questions
The intial velocity of a particle is u (at t=0) and the acceleration is given by f=at. Which of the following relations is valid ?
View SolutionIf the velocity of a paraticle moving along x-axis is given as v=(4t2+3t=1)m/s then acceleration of the particle at t=1sec is :
View SolutionThe position of a particle moving along x- axis is given by x=x0cos2(ωt) . Its when it is at mean position is
View SolutionVelocity of particle moving along x-axis is given as v=(x3−x2+2) m/sec. Find the acceleration of particle at x=2 meter.
View SolutionPosition of particle moving along x-axis is given as x=2+5t+7t2 then calculate :
View SolutionThe velocity v of a particle moving along x - axis varies with ist position (x) as v=α√x, where α is a constant. Which of the following graph represents the variation of its acceleration (a) with time (t)?
View SolutionIf the velocity of a particle moving along x-axis is given as v=(3t2−2t) and t=0, x=0 then calculate position of the particle at t=2sec.
View SolutionThe velocity (υ) of a particle moving along X-axis varies with its position x as shown in figure. The acceleration (a) of particle varies with position (x) as
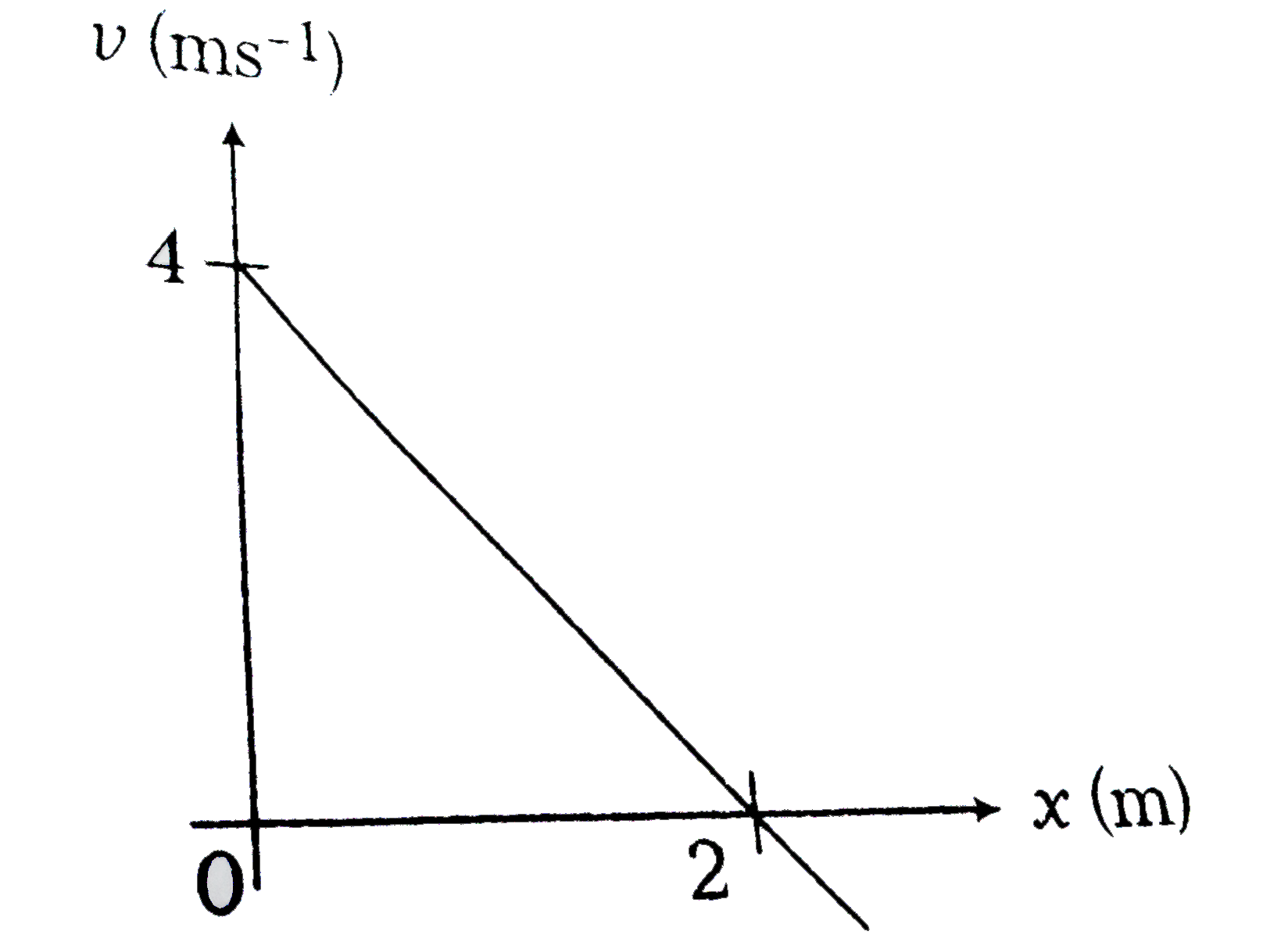
View SolutionThe displacement of a particle along the x-axis is given by x=3+8t+7t2. Obtain its velocity and acceleration at t=2s.
View SolutionA particle is moving along the x-axis with an acceleration a = 2x where a is in ms–2andx is in metre. If the particle starts from rest at x=1 m, find its velocity when it reaches the position x = 3.
View Solution

