The identical solid sphere each having mass m and diameter d are touching each other as shown in figure. Calculate ratio of moment of inertia about an axis (perpendicular to plane of paper) passing through point P ans B as shown in fingure.Given P is centroid of triangle ABC. 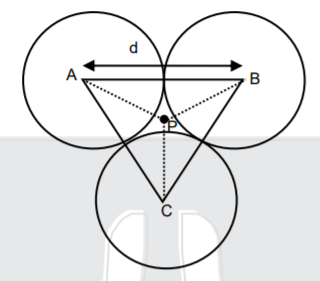
1323
1119
79
1311
The correct Answer is:A
NA
Related Playlists
Similar Questions
Calculate the moment of inertia of a rod of mass M, and length l about an axis perpendicular to it passing through one of its ends.
View SolutionTwo thin discs each of mass M and radius r metre are attached to form a rigid body as shown in figure. The rotational inertia of this body about an axis perpendicular to the plane of disc B and passing through its centre is
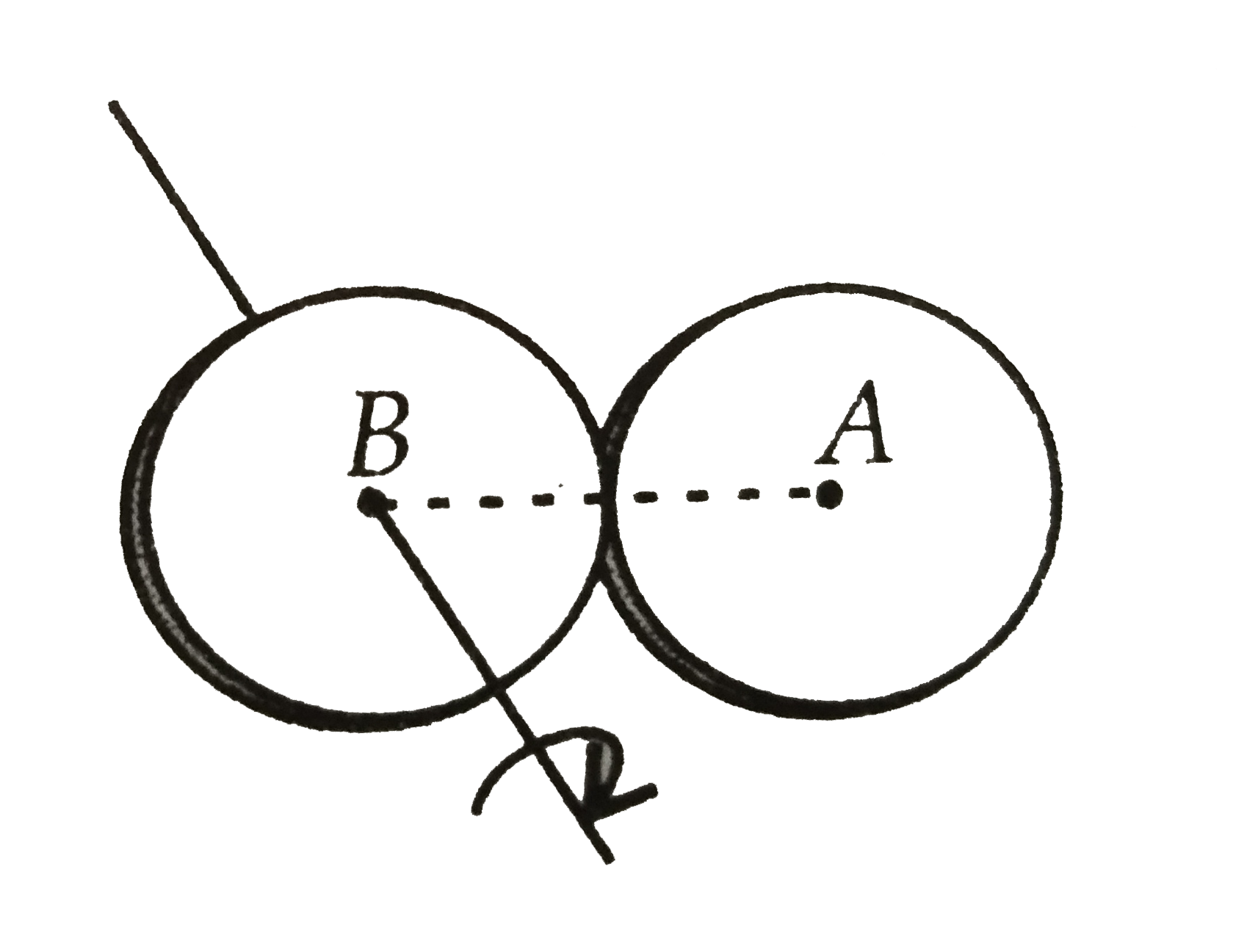 View Solution
View SolutionMoment of inertia of a uniform circular disc about a diameter is I. Its moment of inertia about an axis perpendicular to its plane and passing through a point on its rim will be.
View SolutionCalculate the moment of inertia of a rod of mass 2 kg and length 5 m about an axis perpendicular to it and passing through one of its ends.
View SolutionTwo identical rods each of mass M and length L are kept according to figure. Find the moment of inertia of rods about an axis passing through O and perpendicular to the plane of rods.
 View Solution
View SolutionConsider a uniform square plate of of side and mass m. The moment of inertia of this plate about an axis perpendicular to its plane and passing through one of its corners is -
View SolutionA rod of mass 3 kg and of length 3m is bent in the form of an equilateral triangle. The moment of inertia of the triangle about a vertical axis perpendicular to plane and passing through centre of mass is
 View Solution
View SolutionA thin rod of length 4l, mass 4 m is bent at the point as shown in the figure. What is the moment of inertia of the rod about the axis passing through O and perpendicular to the plane of the paper?
 View Solution
View Solution
A thin rod of length 4l, mass 4 m is bent at the point as shown in the figure. What is the moment of inertia of the rod about the axis passing through O and perpendicular to the plane of the paper?View SolutionThe S-shaped unifrom wire shown in figure has a mass M, and the radius of curvature of each half is R. The moment of inertia about an axis through A and perpendicular to the plane of the paper is:
 View Solution
View Solution


