The e.m.f. of one accumulator is e, its internal resistance is r. Find the e.m.f. ε and the internal resistance 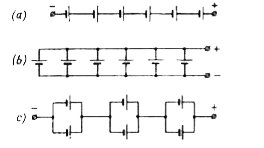
Ri of a battery of n accumulators connected (Fig. 26.10):
(a) in series,
(b) in parallel,
(c) in m series-connected groups of k accumulators, m<n.
k = n/m, where the accumulators are connected in parallel.
The correct Answer is:(a) ε=≠,Ri=nr; (b) ε=e;Ri=r/n;(c)ε=me,Ri=mr/k,=m2r/n.
(a) When the cells are connected in series, their e.m.f. and internal resistances are added.
(b) When the cells are connected in parallel, the e.m.f. remaias unchanged, but the internal conductances are added.
(c) in a mixed connection we calculate first the e.m.i. and the internal resistance of a group, and then the game parameters for the battery as a whole.
Similar Questions
N cells each of e.m.f. E & internal resistance r are grouped into sets of K cells connected in series. The (N/K) sets ae connected in parallel to a load of resistance R, then,
View SolutionN cells each of e.m.f. E & internal resistance r are grouped into sets of K cells connected in series. The (N/K) sets ae connected in parallel to a load of resistance R, then,
View SolutionA cell of e.m.f (E) and internal resistance (r) is connected in series with an external resistance (nr.) then the ratio of the terminal p.d. to E.M.F is
View SolutionA cell of e.mf. E and internal resistance r is connected in series with an external resistance nr. Then, the ratio of the terminal potential difference to E.M.F.is
View SolutionA cell of e.mf. E and internal resistance r is connected in series with an external resistance nr. Then, the ratio of the terminal potential difference to E.M.F.is
View SolutionA battery of e.m.f. E and internal resistance r is connected to a variable resistor R as shown here. Which one of the following is true
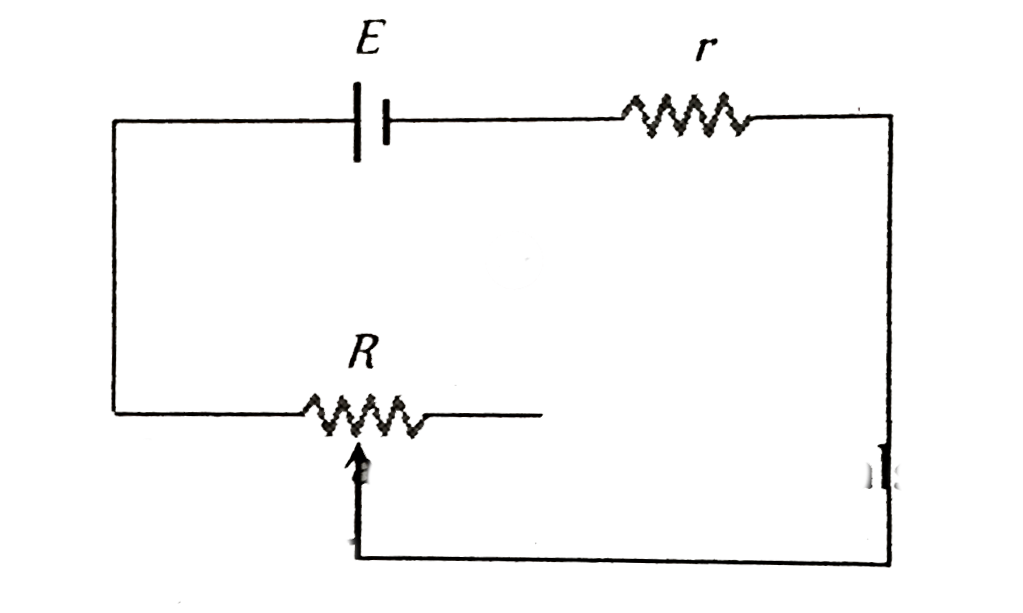 View Solution
View SolutionN batteries each of emf E and internal resistance r are first connected in series and then in parallel to an external resistance R. if current through R is same in both cases then.
View Solutionn identical cells each of e.m.f. E and internal resistance r are connected in series. An external resistance R is connected in series to this combination. The current through R is
View Solutionn identical cells each of e.m.f. E and internal resistance r are connected in series. An external resistance R is connected in series to this combination. The current through R is
View SolutionTwo batteries of e.m.f. E1 and E2 and internal resistance r1 and r2 are connected in parallel. Determine their equivelent e.m.f.
View Solution

