The current of a conductor following through a conductor in terms of the drift speed of electrons is (the symbols have their usual meanings)
I=√nAevd
I=A√nevd
I=neAvd
I=neAvd
The correct Answer is:D
To derive the expression for the current I in a conductor in terms of the drift speed vd of the electrons, we can follow these steps:
Step 1: Understand the definition of current
Current I is defined as the amount of charge Q flowing through a cross-section of a conductor per unit time t. Mathematically, this is expressed as:
I=Qt
Step 2: Relate charge to the number of electrons
The charge Q can be expressed in terms of the number of electrons ne that pass through the conductor. The charge of a single electron is denoted by e. Therefore, the total charge can be expressed as:
Q=ne⋅e
Step 3: Determine the number of electrons passing through a section
To find ne, we need to consider the volume of the conductor that the electrons occupy. If A is the cross-sectional area of the conductor and vd is the drift speed of the electrons, then the volume V of the conductor that passes through a section in time t is given by:
V=A⋅vd⋅t
Step 4: Calculate the number of electrons in that volume
If n is the electron density (number of electrons per unit volume), then the number of electrons ne that pass through the cross-section in time t is:
ne=n⋅V=n⋅(A⋅vd⋅t)
Step 5: Substitute ne into the expression for current
Now substitute ne back into the expression for current:
I=Qt=ne⋅et=(n⋅A⋅vd⋅t)⋅et
Step 6: Simplify the expression
The t in the numerator and denominator cancels out, giving us:
I=n⋅A⋅vd⋅e
Final Expression
Thus, the expression for the current I in terms of the drift speed vd is:
I=n⋅A⋅e⋅vd
Current I is defined as the amount of charge Q flowing through a cross-section of a conductor per unit time t. Mathematically, this is expressed as:
I=Qt
The charge Q can be expressed in terms of the number of electrons ne that pass through the conductor. The charge of a single electron is denoted by e. Therefore, the total charge can be expressed as:
Q=ne⋅e
To find ne, we need to consider the volume of the conductor that the electrons occupy. If A is the cross-sectional area of the conductor and vd is the drift speed of the electrons, then the volume V of the conductor that passes through a section in time t is given by:
V=A⋅vd⋅t
If n is the electron density (number of electrons per unit volume), then the number of electrons ne that pass through the cross-section in time t is:
ne=n⋅V=n⋅(A⋅vd⋅t)
Now substitute ne back into the expression for current:
I=Qt=ne⋅et=(n⋅A⋅vd⋅t)⋅et
The t in the numerator and denominator cancels out, giving us:
I=n⋅A⋅vd⋅e
Thus, the expression for the current I in terms of the drift speed vd is:
I=n⋅A⋅e⋅vd
Topper's Solved these Questions
Similar Questions
Knowledge Check
The correct combination is (symbols have their usual meanings)
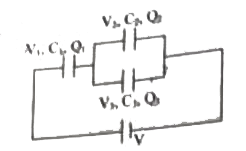 AQ1=Q2=Q3andV1=V2=V3=VBQ1=Q2+Q3andV=V1+V2+V3CQ1=Q2+Q3andV=V1+V2DQ2=Q3andV2=V3
AQ1=Q2=Q3andV1=V2=V3=VBQ1=Q2+Q3andV=V1+V2+V3CQ1=Q2+Q3andV=V1+V2DQ2=Q3andV2=V3Bohr magnetonis given by (symbols have their usual meanings)
A4πmeeh2B4πmeehCeh24πmeDeh4πmeChoose the correct arrangement. The symbols have their usual meanings
A¯v>ump>urmsBurms>¯v>umpCump>¯u>urmsDump>urms>¯v
When current flows through a conductor, then the order of drift velocity of electrons will be
View SolutionWhich of the following is correct ? (symbols have their ususal meanings)
View SolutionFor achromatic combination which of the following is true (symbols have their usual meaning)
View SolutionWhich of the following formula is correct ? [ Where symbols have their usual meaning ]
View SolutionCurrent of 4.8 A is flowing through a conductor. The number of electrons per second will be
View Solution

