The arrangement shown in figure consists of two identical, uniform, solid cylinders, each of mass m, on which two light theads are wound symmetrically.
Find the tensions of each thread in the process of motion. The friction in the axle of the upper cylinder is assumed to be absent.

Let the lower cylinder go down by x when the upper cylinder A rotates through θ and the lower one rotates through θ'. Since both cylinders unwind themselves, therefore
x=R(θ+θ')
We can write a=R(α+α')

Where a=downward acceleration of A
α= angular acceleration of A
α'= angular acceleration of B
Considering the rotational motion of A
τ=2TR=(12MR2)×α⇒4TR
Considering the rotational motion of B
τ=2TR=(12mR2)×a'⇒α'=4TR
Considering the downward motion of B
mg−2T=ma
mg−2T=mR(α+α')=mR(4TR+4TR)
mg−2T=8T⇒T110mg
Related Playlists
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Solved Examples9videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.16videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE2videos
PROPERTIES OF SOLIDS AND FLUIDS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger2videos
RIGID BODY DYNAMICS 2
Similar Questions

In the arrangement shown in figure the mass of the uniform solid cylindrical pulley of radius R is equal to m and the masses of two bodies are equal to m1 and m2. The thread slipping and the friction in the axle of the pulley are supposed to be absent. Find the angular acceleration of the cylinder and the ratio of tensions T1T2 of the vertical sections of the thread in the process of motion.View SolutionFor the arrangement shown in the figure the coefficient of friction between the two blocks is μ. If both the blocks are identical and moving ,then the acceleration of each block is
 View Solution
View SolutionA solid uniform cylinder of mass m performs small oscillations due to the action of two springs of stiffness k each (figure). Find the period of these oscillation in the absence of sliding.
xView SolutionA cylinder of mass m is suspended through two strings wrapped around it as shwon in figure . Find a. the tension T in the string and b. the speed o the cylinder as it falls through a distance h.
 View Solution
View SolutionIn the arrangement shown in figure, the string are light and intextensible. The surface over which blocks are placed is smooth. Find
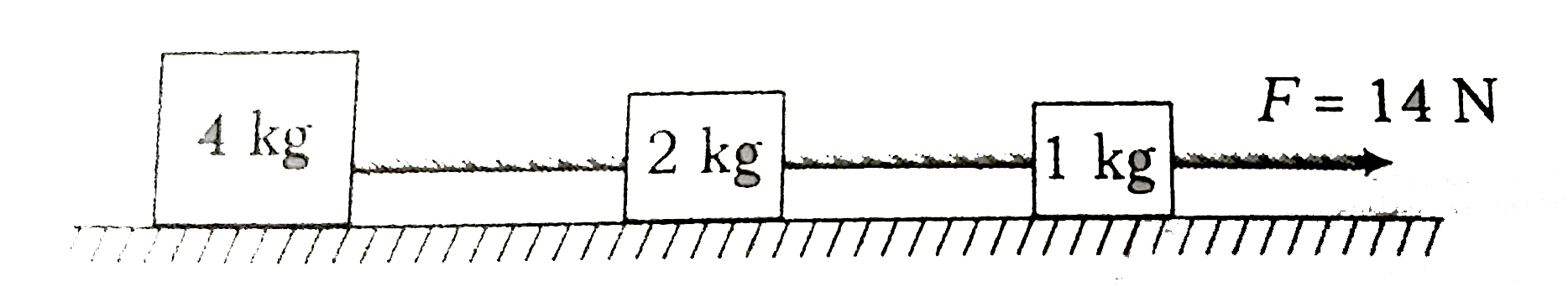
(a) the accelrations of the block
(b) the tension in each string.View SolutionA uniform solid. cylinder A of mass can freely rotate about a horizontal axis fixed to a mount of mass m2. A constant horizontal force F is applied to the end K of a light thread tightly wound on the cylinder. The friction between the mount and the supporting horizontal plane is assumed to be absent. Find the acceleration of the point K.
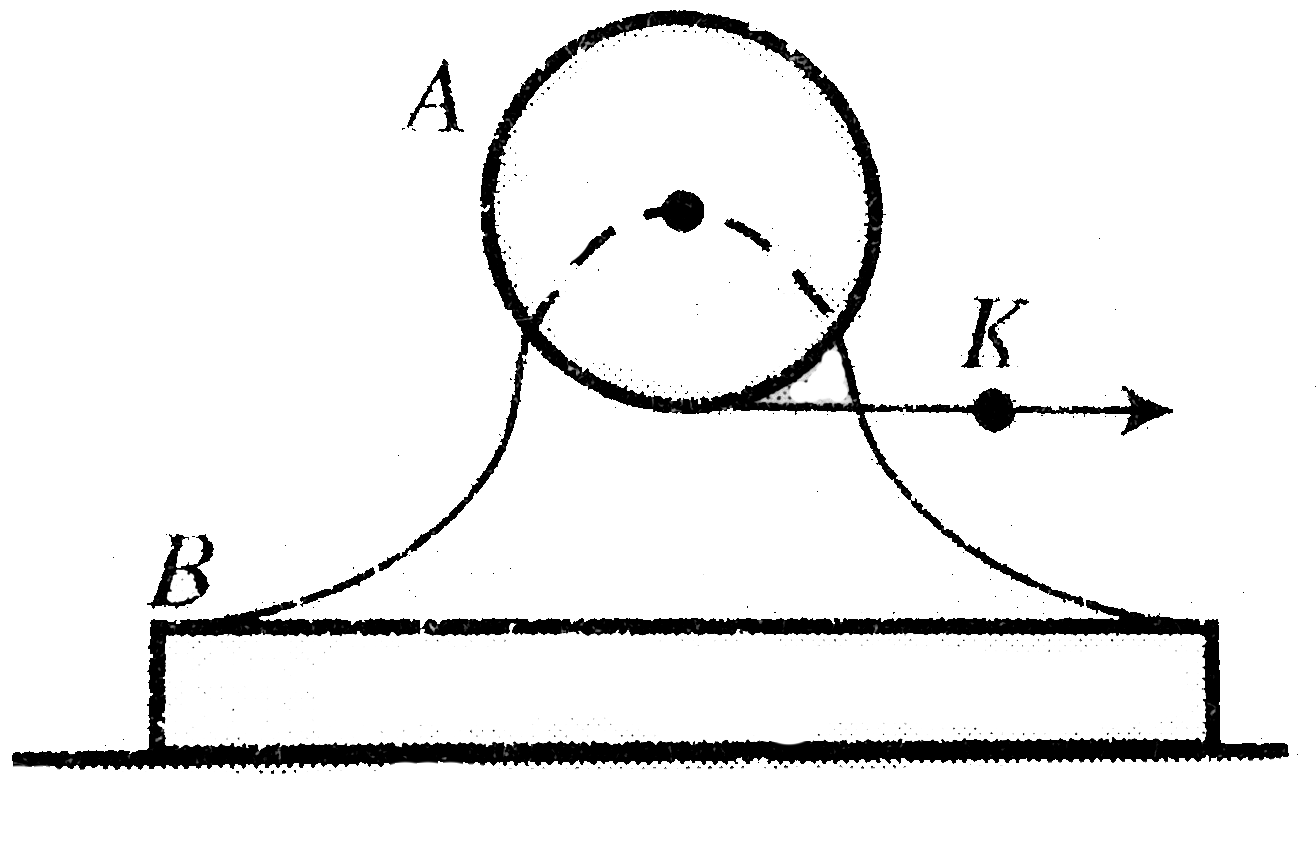 View Solution
View SolutionIn the arrangement shown in figure. The strings are light and inextensible. The surface over which block are placed is smooth.Find
(a) the acceleration of each block,
(b) the tension in each string.
 View Solution
View SolutionConsider a body, shown in figure, consisting of two identical balls, each of mass M connected by a light rigid rod. If an impulse J = MV is imparted to the body at one of its ends what would be it angular velocity?
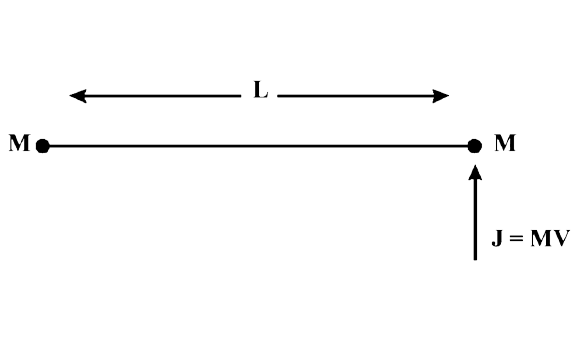 View Solution
View SolutionConsider a body, shown in figure, consisting of two identical balls, each of mass M connected by a light rigid rod. If an impulse J = MV is imparted to the body at one of its ends what would be it angular velocity?
 View Solution
View SolutionIn the arrangement shown in fig., mass of the rod M exceeds the mass m of the ball. The ball has an opening permitting it to slide along the thread with some friction. The mass of the pulley and the friction in its axle are negligible. At the initial moment, the ball was located opposite the lower end of the rod. When set free, both bodies began moving with constant accelerations. Find the friction force between the ball and the thread if t seconds after the beginning of motion, the ball got opposite to the upper end of the rod. The rod length equals l.
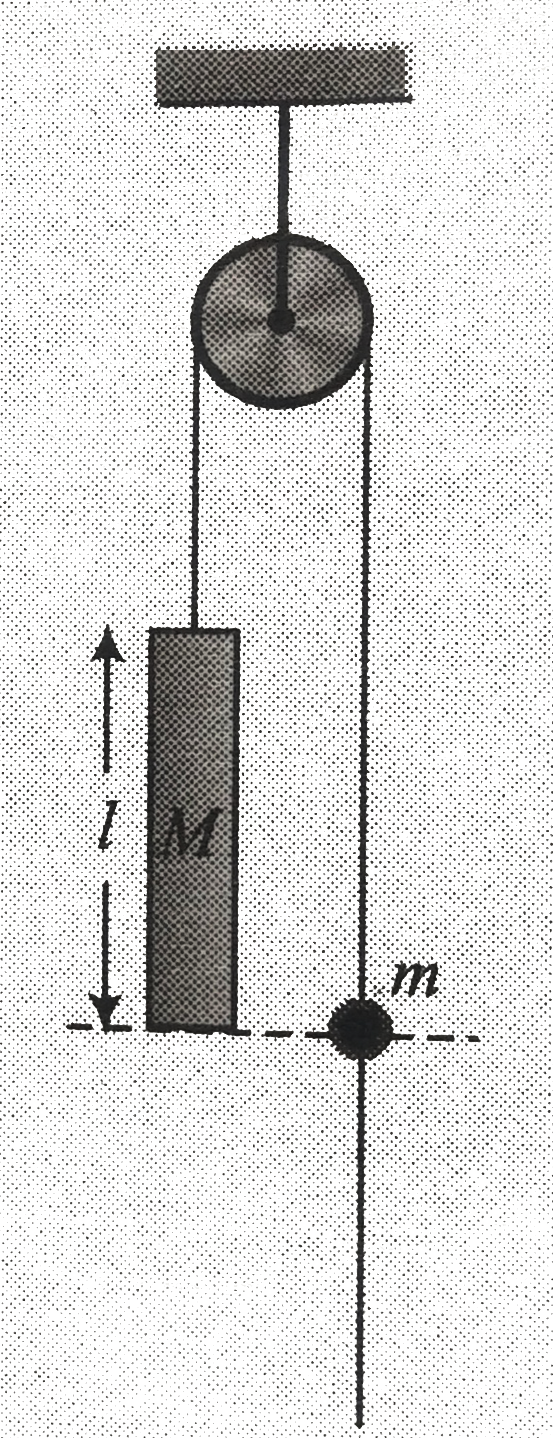 View Solution
View Solution


