Test if the following equations are dimensionally correct:
(a) $h = \frac{2 S cos θ}{ρ r g}$
(b). $ν = \sqrt{\frac{P}{ρ}}$ ,
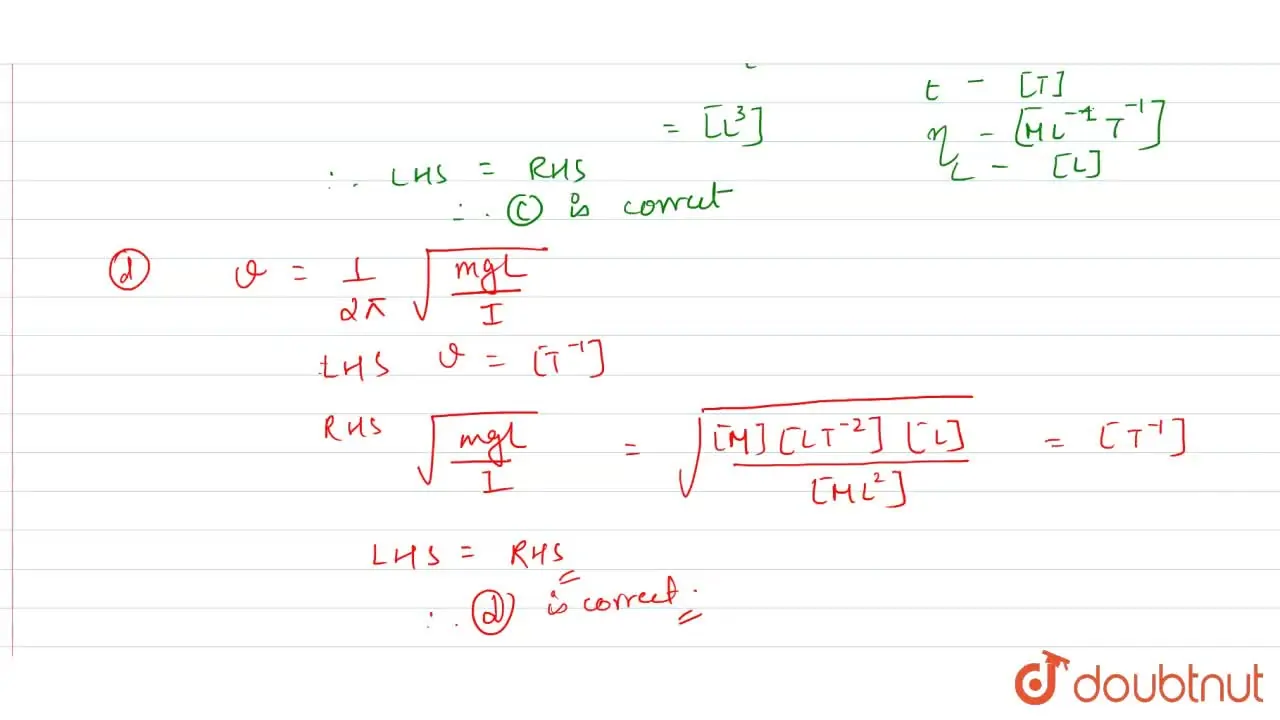
(c). $V = \frac{π P r^{4} t}{8 η l},$
(d). $v = \frac{1}{2 π} \sqrt{\frac{m g l}{I}}$
where h height, S= surface tension, $ρ$ = density, P= pressure, V=volume, $η$ = coefficient of viscosity, v= frequency and I = moment of inertia.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, B, C, D

a. $h = \frac{2 S cos θ}{ρ r g} < b r > L H S = h = [L]$
Surface Tension
$S = \frac{F}{L} = \frac{M T^{- 2}}{L} = [M T^{- 2}] < b r > D e n s i t y < b r > ρ = \frac{M}{V} = [M L^{- 3} T^{0}], R a d i u s < b r > r = [L], g = [L T^{- 2}]$
Now
$R H S = \frac{2 S cos θ}{ρ r g} < b r > = \frac{[M L^{- 2}]}{[M L^{- 3} T^{0}] [L] [L T^{- 2}]} < b r > = [M^{0} L^{1} M^{0}] = [L]$ Hence the relation is correct., b. Velocity, $v = \sqrt{(\frac{P}{ρ})} < b r > L H S = D e m e n s i o n o f v, = [L T^{- 1}], D i m e n s i o n o f P = \frac{F}{A} = [M L^{- 1} T^{- 2}] < b r > D i m e n s i o n o f ρ = \frac{m}{V} = [M L^{3}], R H S = \sqrt{\frac{P}{ρ}}, ⎤ ⎥ ⎦ {[\frac{[M L^{- 1} T^{- 2}]}{[M L^{- 3}]}]}^{\frac{1}{2}}, = {[L^{2} T^{- 2}]}^{\frac{1}{2}}, = [L T^{- 10} = L H S$ Hence relation is correct.
c. $V = \frac{(π P r^{4} t)}{(8 η l)}$ , LHS= Dimension of $V = [L^{3}]$
Dimension of $P = [M L^{- 1} T^{- 2}], r^{4} = [L^{4}], t = [T]$ , Coefficient of viscosity
$= [M L^{- 1} T^{- 1}] < b r > D i m e n s i o n s o f R H S = \frac{(π P r^{4} t)}{8 η l}) < b r > = \frac{[M L^{- 1} T^{- 2}] [L^{4}] [T]}{[M L^{- 1} T^{- 1}] [L]} < b r > = L^{3} = L H S$
Hence the relation is correct. d. $v = \frac{1}{2 π} \sqrt{\frac{m g l}{I}},$ RHS= dimension fo $v = [T^{- 1}], R H S = \sqrt{\frac{m g l}{I}} < b r > = \sqrt{} M ⎤ ⎥ ⎦ [L T^{- 2}] [L] \frac{)}{[M L^{2}]}, {[\frac{[M L^{2} T^{- 2}]}{[M L^{2}]}]}^{\frac{1}{2}} < b r > = [T^{- 1}] = L H S$
Hence the relation is correct.

Updated on:21/07/2023

|

Class 11 PHYSICS PHYSICAL WORLD

Topper's Solved these Questions

Similar Questions

Knowledge Check

Which of the following relationships between partial pressure , volume and temperature is correct ?
(i) $P = \frac{n R T}{V}$
(ii) $P_{total} = P_{1} + P_{2} + P_{3}$
(iii) $P_{total} = (n_{1} + n_{2} + n_{3}) \frac{R T}{V}$
A(i) and (ii)
B(i) and (iii)
C(ii) and (iii)
D(i) , (ii) and (iii)

HC VERMA ENGLISH-INTRODUCTION TO PHYSICS-Exercises

Home
Ask Doubt
Profile