State parallelogram law of vectors. Derive an expression for the magnitude and direction of the resultant vector.
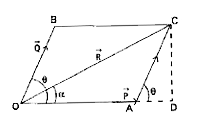
Statement : If two vectors acting at a point are represented by the adjacent sides of a parallelogram in magnitude and direction, then their resultant is represented by the diagonal of the parallelogram in magnitude and direction drawn from the same point.
Explanation : Let two forces →P and →Q act at a point O. Let θ be the angle between two forces. Let the side OA=→P and OB=→Q. The parallelogram OACB is completed. The points O and C are joined.
Now OC=→R
Resultant magnitude :
In fig −−→OA=→P,−−→OB=→Q,−−→OC=→R
In the triangle COD,OC2=OD2+CD2
OC2=(OA+AD)2+CD2(∵OD=OA+AD)
OC2=OA2+AD2+2OA.D+CD2
OC2=OA2+AC2+2OA.AD ..........(1)
from ΔleCAD,AD2+CD2=AC2
From ΔleCAD,cosθ=ADAC ...........(2)
AD=ACcosθ
∴R2=P2+Q2+2PQcosθ
R=√P2+Q2+2PQcosθ ...........(3)
Resultant direction :
Let α be the angle made by the resultant vector →R with →P
Then tanα=CDOD
tanα=CDOA+AD ..........(4)
In the triangle CAD, sinθ=CDAC
CD=ACsinθ
CD=Qsinθ ...........(5)
∴tanα=QsinθP+Qcosθ(∵AD=Qcosθ)
α=tan−1(QsinθP+Qcosθ) ..............(6)
Similar Questions
Find the magnitude and direction of the resultant of given vectors
 View Solution
View SolutionState parallelogram law of vector addition. Find analytically the magnitude and direction of resultant vector. Apply it to find the resultant when,
(i) Two vectors are parallel to each other
(ii) Two vectors are perpendicular to each otherView SolutionState parallelogram law of vector addition. Find analytically the magnitude and direction of resultant vector. Apply it to find the resultant when,
(i) Two vectors are parallel to each other
(ii) Two vectors are perpendicular to each otherView SolutionState parallelogram law of vectors addition .Find analytcallly the magnitude and direction of resultant vector, When (i) two vectors are parallel to each other (ii) two vectors are perpendicular to each other.
View SolutionState parallelogram of law of vector addition .
View SolutionParallelogram Law of Vector Addition
View SolutionState triangle law of vectors addition. Find analytically the magnitude and dirction of resultant vector.
View SolutionParallelogram law of addition of vectors
View SolutionTwo vectors →a&→b have equal magnitudes of 10 m ,. Find the magnitude and direction of the resultant vector .
View SolutionParallelogram law of vectors is applicable to the addition of :
View Solution

