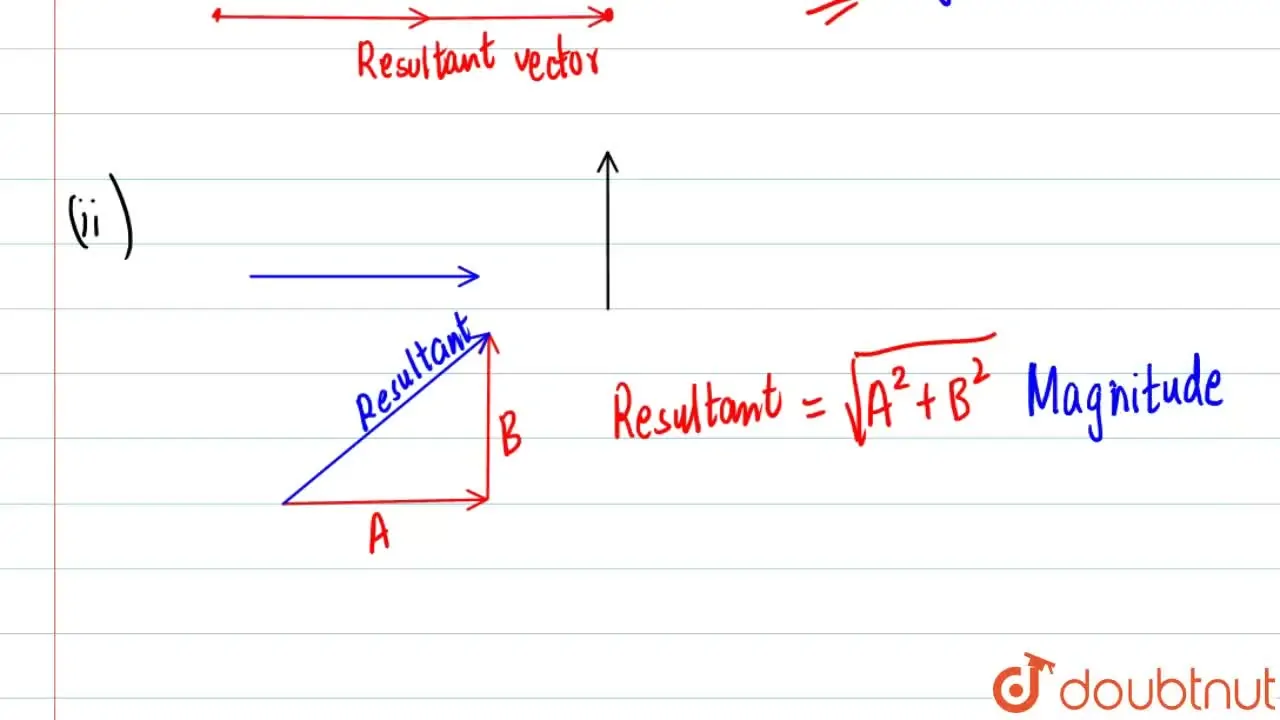
State parallelogram law of vector addition. Find analytically the magnitude and direction of resultant vector. Apply it to find the resultant when,
(i) Two vectors are parallel to each other
(ii) Two vectors are perpendicular to each other
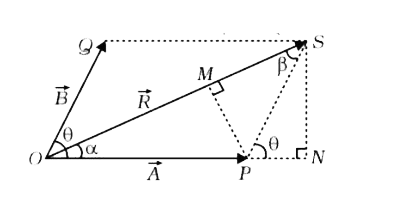
Parallelogram law of vector addition: If two vectors, acting simultaneously at a point, can be represented both in magnitude and direction by two adjacent sides of a parallelogram, the resultant is represented completely, both in magnitude and direction, by the diagonal of the parallelogram passing through that point. Let OP and OQ represent the two vectors →A and →B and making an angle θ Then, using the parallelogram method of vector addition, OS represents the resultant vector →A and →rB making an angle θ then using the parallelogram method of vector addition os represent →R=→A+→B
SN is normal to op and PM is normal to os from the geometry of hte figure
OS2=ON2+SN2
but ON=OP+PN=A+Bcosθ
in △ OSN , SN =OS sinα=Rsinα and
In △ PSN ,SN =PS sinθ=Bsinθ
where R isd given by equation (i) or tan α=SNOP+PN=BsinθA+Bcosθ
(i) given θ=0∘
∴R=√A2+B2+2ABcos(0∘)=A+B,tanα=Bsinθ∘A+Bcos0θ=0orα=0∘
(ii) Given : θ=π2∴R=√A2+B2+2ABcos(π)2=−√A2+B2
α=tan−1(B)A
Related Playlists
- BOOK - VMC MODULES ENGLISHCHAPTER - INTRODUCTION TO VECTORS & FORCES EXERCISE - level 175videos
INTRODUCTION TO VECTORS & FORCES
- BOOK - VMC MODULES ENGLISHCHAPTER - INTRODUCTION TO VECTORS & FORCES EXERCISE - level 265videos
INTRODUCTION TO VECTORS & FORCES
- BOOK - VMC MODULES ENGLISHCHAPTER - GRAVITATIONEXERCISE - JEE Advance (Archive) TRUE/FALSE1videos
GRAVITATION
- BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN - 5EXERCISE - PART I : PHYSICS (SECTION - 2)5videos
JEE MAIN - 5
Similar Questions
State parallelogram of law of vector addition .
View SolutionFind the magnitude and direction of the resultant of given vectors
 View Solution
View SolutionTwo vectors →P and →Q that are perpendicular to each other if :
View SolutionFind the magnitude and direction of the resultant of two vectors A and B in the terms of their magnitudes and angle θ between them.
 View Solution
View SolutionTwo vector A and B have equal magnitudes. Then the vector A+B is perpendicular to
View SolutionIn the above problem, this horizontal distance between the two fragments when their position vectors are perpendicular to each other is
View Solution(a) Write law of parallelogram of vector and obtain the expression for the resultant of two vectors acting in two different directions.
View SolutionIs it possible that dot product of two vectors is zero even if they are not perpendicular to each other ?
View SolutionIn Q-2, if vectors are perpendicular to each other then find the value of λ.
View SolutionTwo vectors 3 units and 5 units are acting at 60∘ to each other .What is the magnitude and direction of the resultant ?
View Solution