State and prove parallel axes theorem.
Text Solution
Statement : The moment of inertia of a plane lamina about an axis is equal to the sum of the moment of inertia about a parallel axis passing through the centre of mass and the product of its mass and square of the distance between the two axes i.e., I=Ig+Mr2I
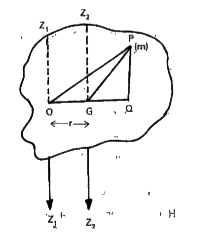
Let Ig is the moment of inertia of the plane lamina about the axis Z2 passing through the centre of mass.
I0 is the moment of inertia of the plane lamina about an axis Z1.
Let M be the mass of the lamina and r be the distance between the two axes. Then I0=Ig+mr2.
Proof : Let a particle of mass m is situated at P. Moment of inertia about the axis pass in through 0(2) is dl=mop2orI=Σmop2
Join the lines r PO and PG and draw the line PQ and Join with the line extending from OG.
From the triangle POQ, OP2=OQ2+PQ2
OP2=(OG+GQ)2+PQ2∵OQ=OG+GQ
OP2=OG2+2OG.GQ+(GQ2+PQ2)
OP2=OG2+2OG.GQ+GP2
OP2=OG2+GP2+2OG.GQ
Multiplying with Σm on both sides ∵ From the ΔlePGQ, GP2=PQ2+GQ2
ΣmOP2=ΣmOG2+ΣmGP2+ΣmOG.GQ
but ΣmOG2=Mr2
(∵OG is constant and Σm = M total mass of the body)
ΣmGP2=Ig
ΣmOP2=I0
∴I0Mr2+Ia+2rΣmGQ
Σm.GQ=0 [∵ The moment of all the particles about the centre of mass is always zero]
I0=Ig+Mr2
Thus the theorem is proved.
|
Updated on:21/07/2023
Similar Questions
State and prove Bernoulli's theorem.
View SolutionState (i) parallel axes theorem and (ii) perpendicular axes theorem.
View SolutionState and prove the Pythagoras theorem.
View SolutionState and prove the Pythagoras theorem.
View SolutionState and prove theorem of parallel axes.
View SolutionState and prove theorem of parallel axes.
View SolutionState theorem of parallel axes.
View SolutionState and prove Bernouli's theorem.
View SolutionState theorem of parallel axes and therom of perpendi cular axes about moment of inertia.
View SolutionState and prove Gauss's law in electrostatics.
View Solution

