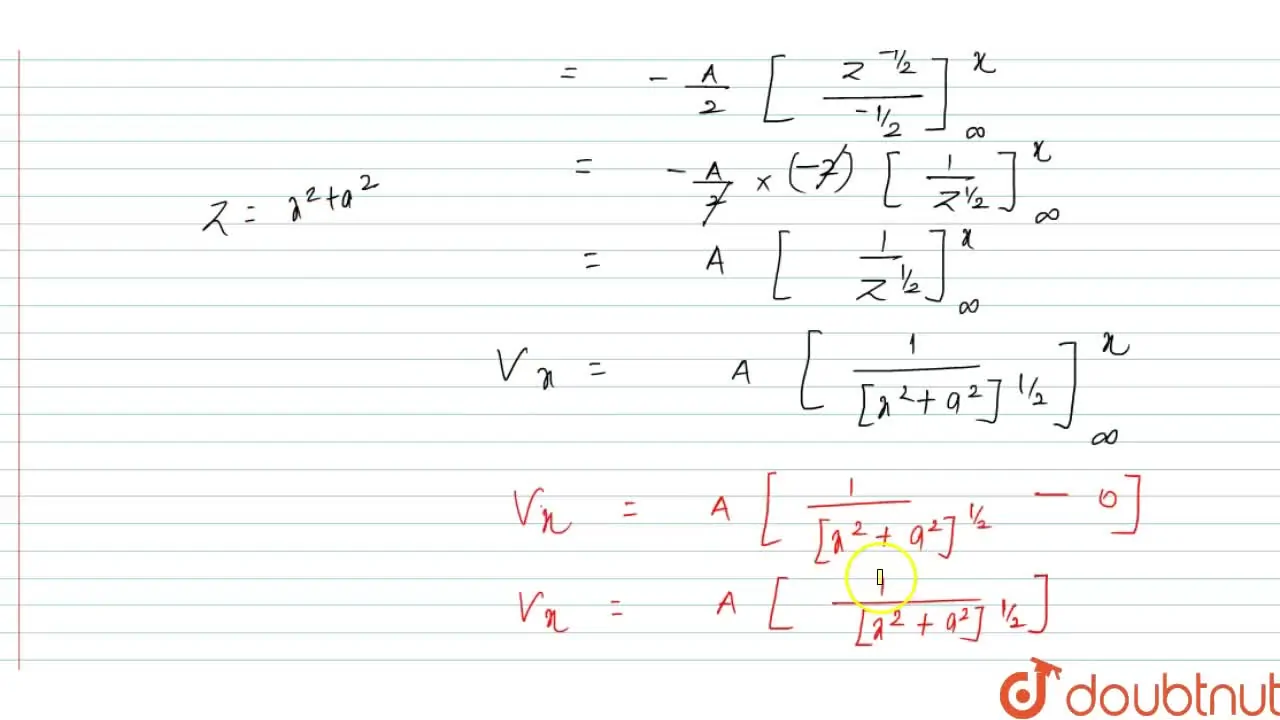On the x - axis and at a distance x from the origin, the gravitational field due to a mass distribution is given by Ax(x2+a2)3/2 in the x - direction. The magnitude of gravitational potential on the x - axis at a distance x, taking its value to be zero at infinity , is :
A(x2+a2)1/2
A(x2+a2)3/2
A(x2+a2)3/2
A(x2+a2)1/2
Step by step video & image solution for On the x - axis and at a distance x from the origin, the gravitational field due to a mass distribution is given by (Ax)/((x^2+a^2)^(3//2)) in the x - direction. The magnitude of gravitational potential on the x - axis at a distance x, taking its value to be zero at infinity , is : by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
Similar Questions
The gravitational field due to a mass distribution is E=K/x3 in the x - direction. ( K is a constant). Taking the gravitational potential to be zero at infinity, its value at a distance x is
View SolutionThe gravitational potential due to a mass distrubution is given by V=8xx2+p2. Find gravitational field at x = p.
View SolutionThe gravitational field due to a mass distribution is E=Ax2 in x-direction. Here, A is a constant, Taking the gravitational potential to be zero at infinity, potential at x is
View SolutionThe gravitational field due to a mass distribution is given by l=kx−3/2 in x-direction, where k is a positive constant. Taking potential to be zero at infinity, find its value at a distance x.
View SolutionThe gravitational potential due to a mass distribution is V=A√x2+a2. Find the gravitational field.
View SolutionThe gravitational potential due to a mass distribution is V=3X2Y+Y3Z. Find the gravitational filed.
View SolutionThe gravitational field due to a mass distribution is given by →l=kx2ˆi, where k is a constant. Assuming the potential to be zero at infinity, find the potential at a point x = a.
View SolutionCircle(s) touching x-axis at a distance 3 from the origin and having an intercept of length 2√7 on y-axis is (are)
View SolutionGravitational field intensity is given byE=Ax(A2+x2)32 then find out potential at x (Assume potential at infinity = 0)
View SolutionFind the intensity of gravitational field at a point lying at a distance x from the centre on the axis of a ring of radius a and mass M.
View Solution