Initially the system shown in figure is in equilibrium. At the moment, the string is cut the downward of a1 and a2 are.
 .
.
(a) zero and zero
(b) 2g and zero
(c) g and zero
(d) None of the above
The correct Answer is:B
T=2mg
As soon as string is cut T (on A) suddenly becomes zero . Therefore a force of 2mg on upward direction on A suddenly becomes zero.
So net force on it will become 2mg downwards.
∴a1=2mgm=2g (downwards)
Spring force dorce not become instantly zero so acceleration of B will not change abruptly.
or a2=0
Related Playlists
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 More Than One Correct9videos
WORK, ENERGY & POWER
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Subjective15videos
WORK, ENERGY & POWER
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 1 subjective27videos
WORK, ENERGY & POWER
- BOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question11videos
WAVE MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY33videos
WORK, ENERGY AND POWER
Similar Questions
For the system shown in figure, the tensions in the string
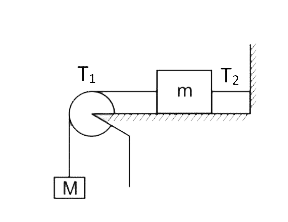 View Solution
View SolutionThe system shown in figure is initially in equilibrium. What is the acceleration of B just after the string connecting B to ground is cut ?
 View Solution
View SolutionThe system shown in the figure is in equilibrium at rest. The spring and string are massless Now the string is cut. Find the acceleration of the blocks just after the string is cut.
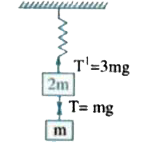 View Solution
View SolutionSystem shown in fig is in equilibrium and at rest. The spring and string are massless now the string is cut. The acceleration of mass 2m and m just after the string is cut will be:
 View Solution
View SolutionSystem shown in fig is in equilibrium and at rest. The spring and string are massless now the string is cut. The acceleration of mass 2m and m just after the string is cut will be:
 View Solution
View SolutionThe system shown in the figure is initially in equilibrium. A is of mass 2 m and B,C D and E are of mass m Certain actions are performed on the system. Every action has been taken individually when the system is intact. Find the direction and magnitude of acceleration of the blocks after each action of the following actions has been taken
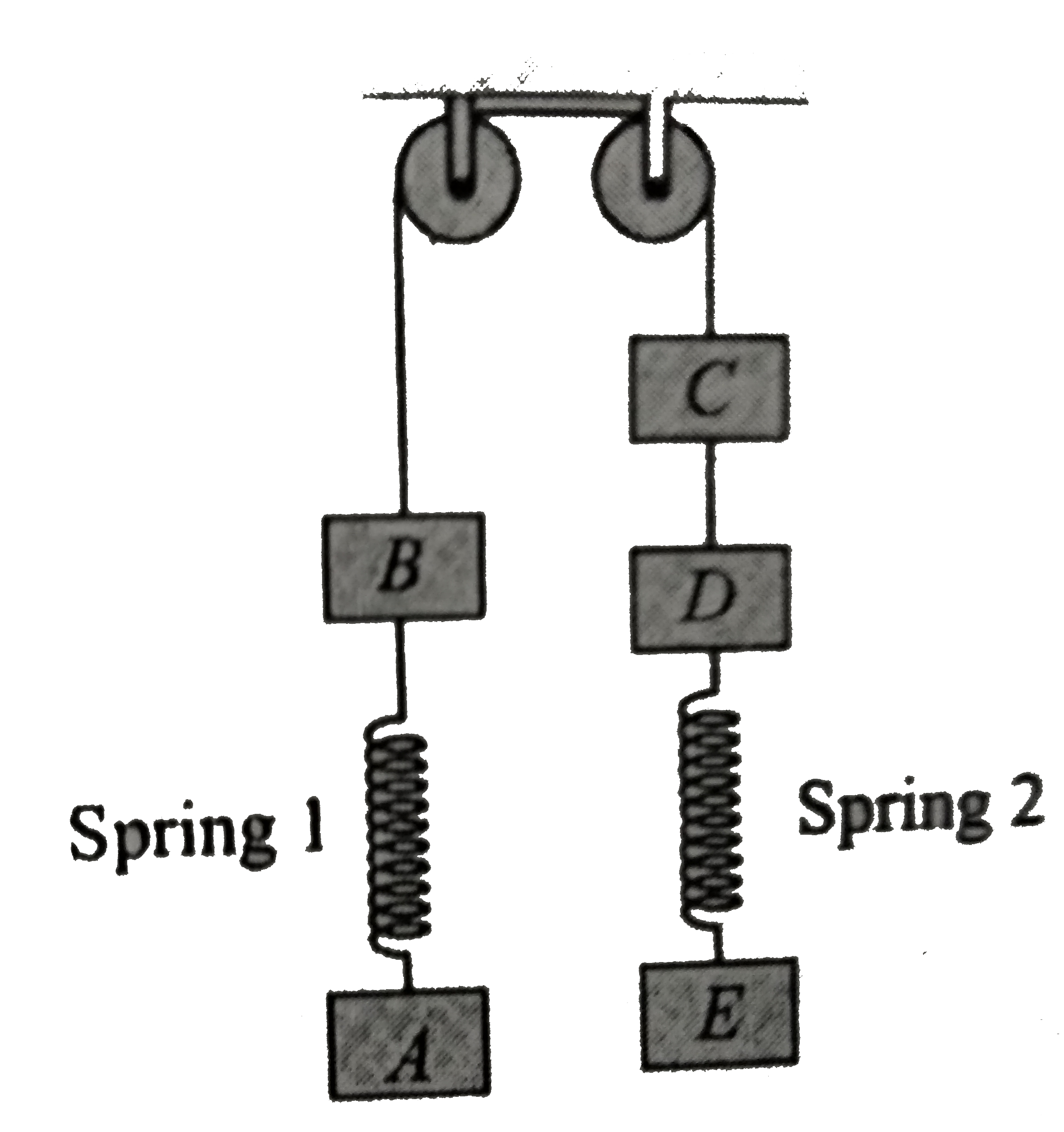
(i)Spting 1 is cut(ii)Spring 2 is cut(iii)String between C and D is cut.(iv)String between B and C is cut.View SolutionSystem shown in figure is equilibrium in vertical plane. Consider the string and spring to be massless. Both the blocks have same mass 'm'. If the string is cut, then just after cutting it :
 View Solution
View SolutionAcceleration of pulleys and blocks are as shown in the figure. All pulleys & strings are massless & frictionless magnitude of aA and aB are :
 .View Solution
.View SolutionFigure shown two pulley arrangments for lifting a mass m . In case-1, the mass is lifting by attaching a mass 2m while in case-2 the mass is lifted by pulling the other end with a downward force F=2mg . If aa and ab are the accelerations of the two masses then (Assumme string is massless and pulley is ideal).
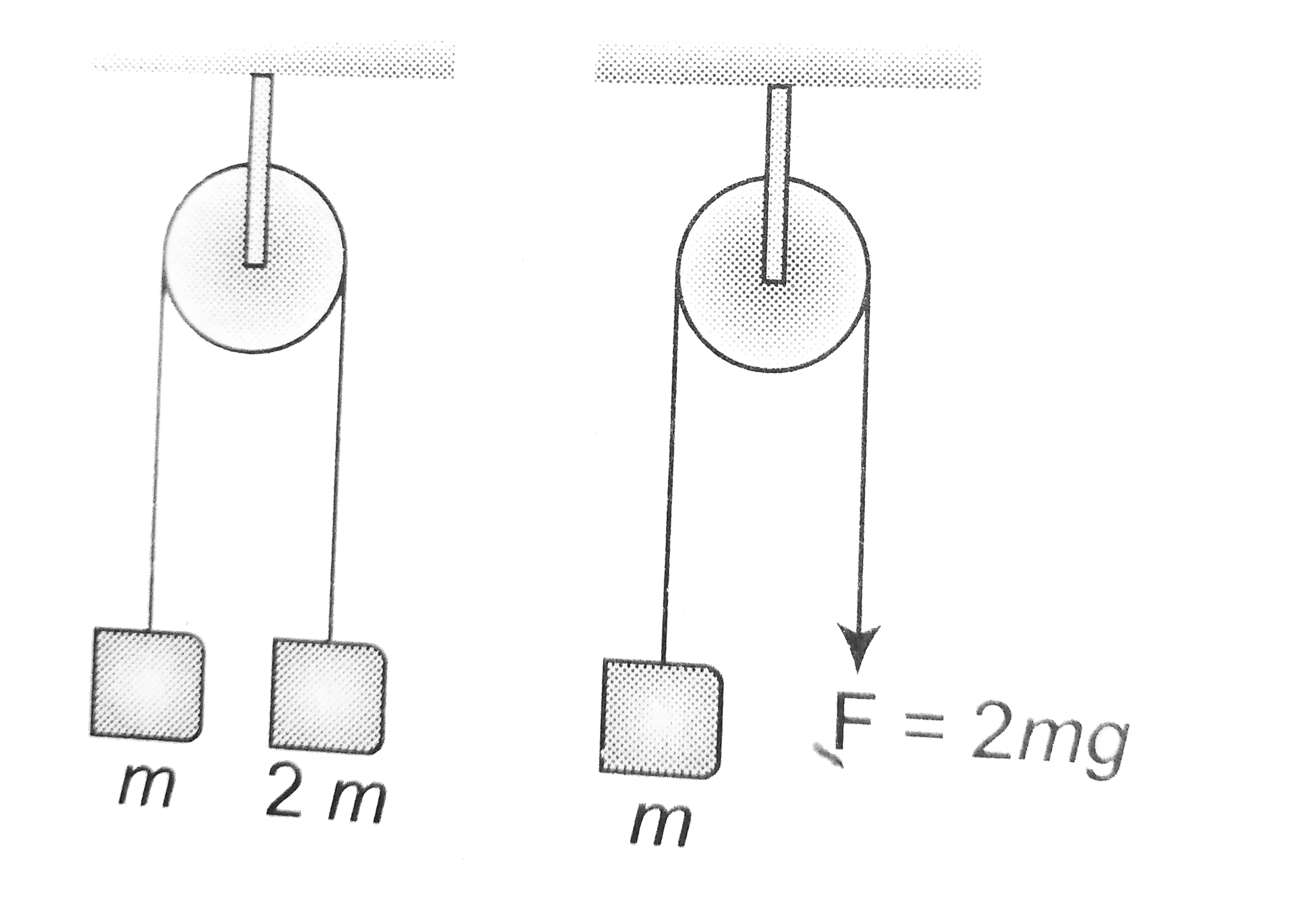 View Solution
View SolutionFind the tensions in the string (1),(2) and (3) and the acceleration of the mass 'm' just after ( initially system is in equilibrium and at rest, pulley, string, spring are light ):

(a) string (1) is cut
(b) string (2) is cut
(c) string (3) is cutView Solution


