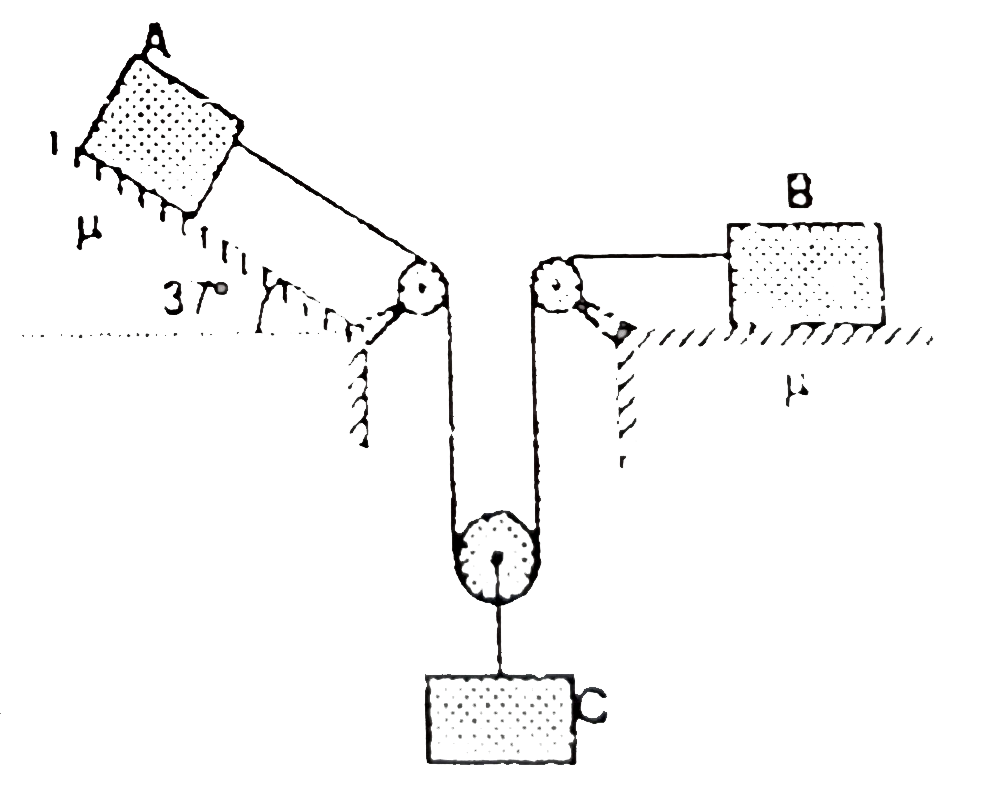
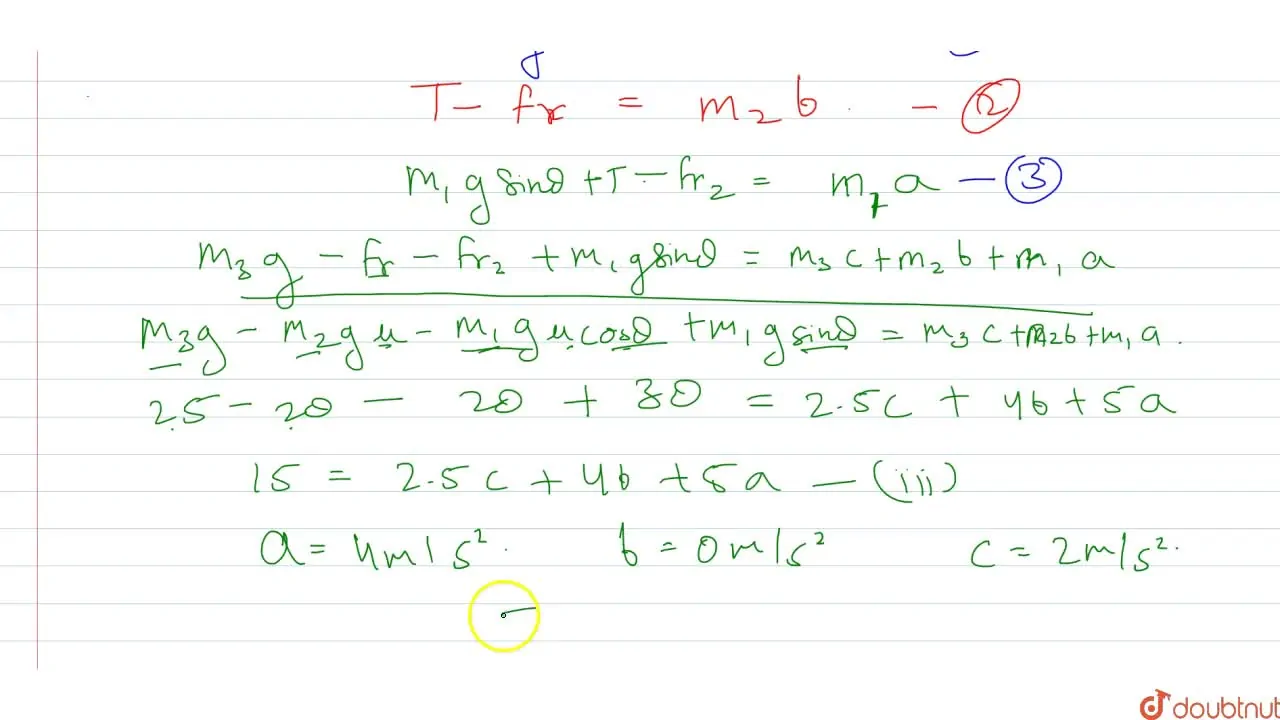In the arrangement shown in figure pulleys are mass of block A,b and C is m1=5kgm2=4kg and m3=2.5kg respectively .Co-efficient acceleration of friction for both the plane is μ=0.50 Calculate acceleration of which block when system is released from rest
The correct Answer is:a1=4ms−2 b. a2=0 c. a3=2ms−2
When the system is released , block C tries to move vertically downward due to its own weight in the process blocks A and B are pulled by tension in the thread Hence block A tries to move down the plane and block B leftward.
Let the magnitude of acceleration of A and B be a and b respectively along the direction dicassed above . Then acceleration of block C will be (a+b2) downward considering free body diagram
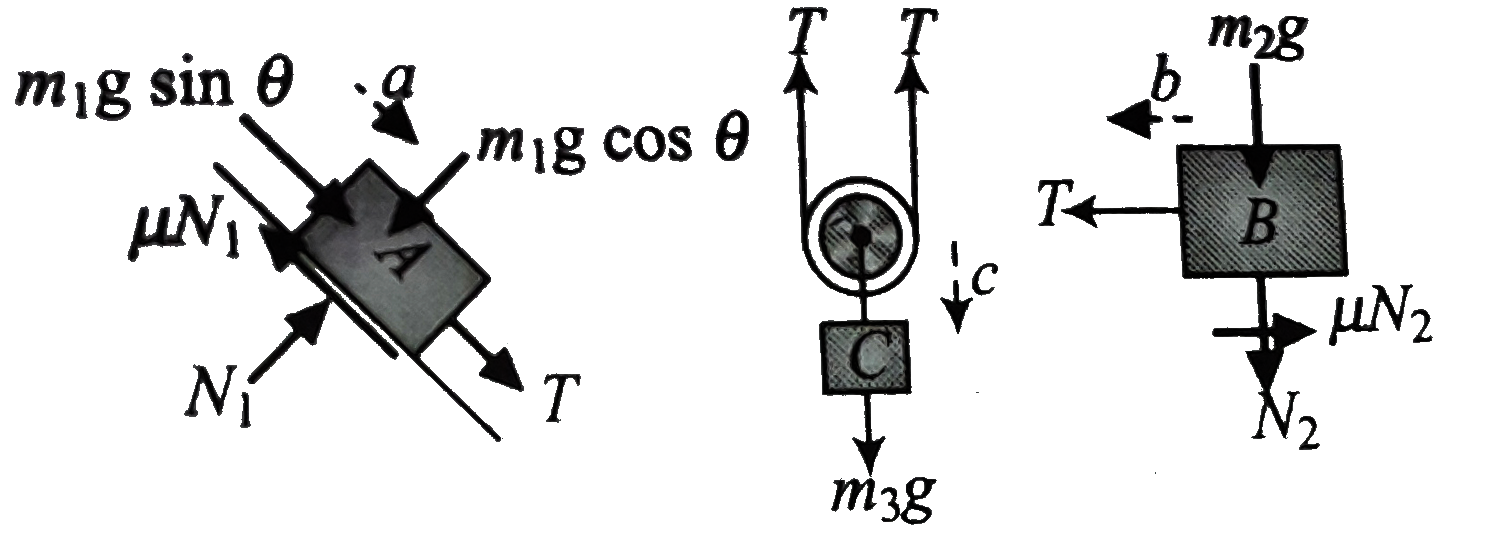
For force on block A N1=m2gcosθ=40N
m2gsinθ+T−μN1=m1aorT−10=5a...(i)
For force on block C
m2g−2T=m3(a+b2)⇒25−2T=1.25(a+b)....(ii)
For force on blockB
N2=m2g=40N
T−μN2=m2bor(T−20)=4b...(iii)
From above three equations
T=46041N,a=17441ms−2 and b=9041ms−2
Negative value of b indicans that block b does not slide along the assumed direction which is leftward from geomery it is clear that B camon move rightward . Therefore the block B remain stationary B is due to the fact tension T in thread is less than the limitiung friction μN2
Hence b=0
Considering free body diagram again

for force on block AN1=m2gcosθ=40 newton
T+m2gsinθ−μN1=m1a
or (T+10)=5a....(iv)
For force on blocks Cm2g−2T=m3(a2)
(25−2T)=1.25a...(vi)
From Eqs (v) and (vi)
T=10Nanda=4ms−2
Acceleration of block Aa1=4ms−2
Acceleration of block Ba2=0
Acceleration of block CBa3=2ms−2
Related Playlists
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Single Correct87videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Multiple Correct2videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Exercise 7.327videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer5videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE2videos
PROPERTIES OF SOLIDS AND FLUIDS
Similar Questions
In the arrangement shown in the figure pulleys are small, light and frictionless, threads are inextensible and mass of blocks A, B and C is m1=5kg, m2=4kg and m3=2.5kg respectively and co-efficient of friction for both the planes is μ=0.50. Calculate the acceleration of block A (in m/s2) when the system is released from rest. (g=10m/s2)
 View Solution
View SolutionIn the arrangement shown in figure mass of blocks A,B and C is 18.5kg.8kg and 1.5kg respectively . The bottom surface of A is A is smooth while coefficient of friction that between block A and C is μ1=1/3 between B and floor is μ2=1/5 System is relased from rest r=0 and pulley are light and friction Calculate acceleration of block A ,B and C
 View Solution
View SolutionPulleys shown in the system of the figure are massless and friction less. Threads are inextensible. Mass of block A, B and C are m1kg,m2=4kg and m3=2.75kg, respectively .Calculate acceleration of A block
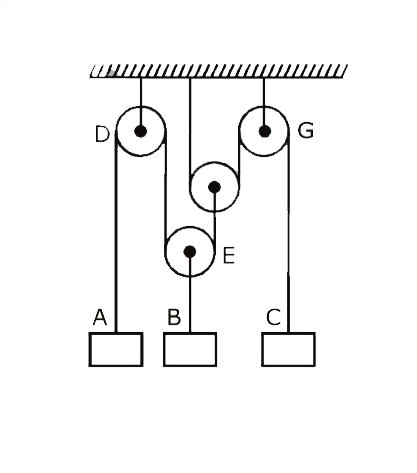 View Solution
View SolutionIn the figure-2.205 shown in blocks A, B and C has masses mA=5kg,mB=5kg and mC=10kg respectively, find the acceleration of the three blocks. Assume all pulleys and strings are ideal. (Take g=10m/s2)
 View Solution
View SolutionPulleys shown in the system are massless and fricionless. Threads are inextensible. The mass of blocks A, B, and C are m1=2kg,m2=4kg, and (m3)=2.75kg, respectively. Calculate the acceleration of each block.
 View Solution
View SolutionIn the figure shown, if friction coefficient of block 1 kg and 2kg with inclined plane is μ1=0.5 and μ2=0.4 respectively, then
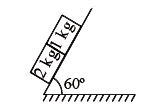 View Solution
View SolutionThe acceleration of 3 kg block in the arrangement shown in the diagram ,when the given system is released from rest is
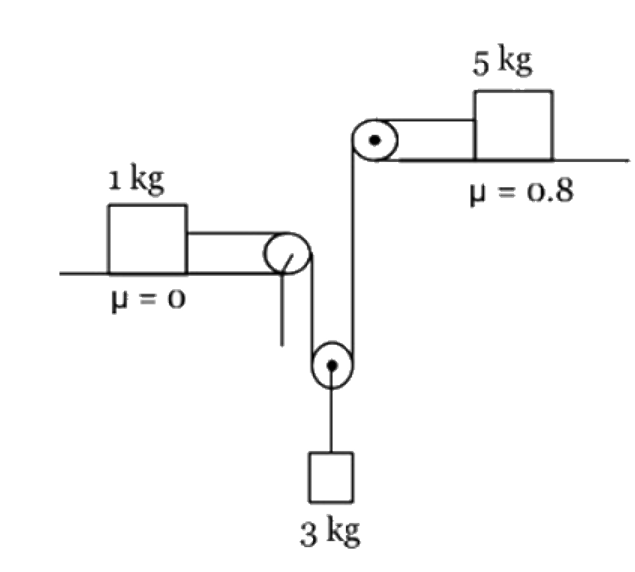 View Solution
View SolutionThree blocks of masses m1=1kg,m2=2kg and m3=3kg are placed in contact on a horizontal frictionaless plane as shown in figure. A force of 12 N is applied on m1. Acceleration of the system is
 View Solution
View SolutionTwo block A and B are arrenged as shown in figure (mA=5kgandmB=10kg) Find the acceleration of blocks if F=40N
 View Solution
View SolutionIn the system shown in the figure all surfaces are smooth and both the pulleys are mass less. Block on the incline surface of wedge A has mass m. Mass of A and B are M = 4 m and M0=2 m respectively. Find the acceleration of wedge A when the system is released from rest.
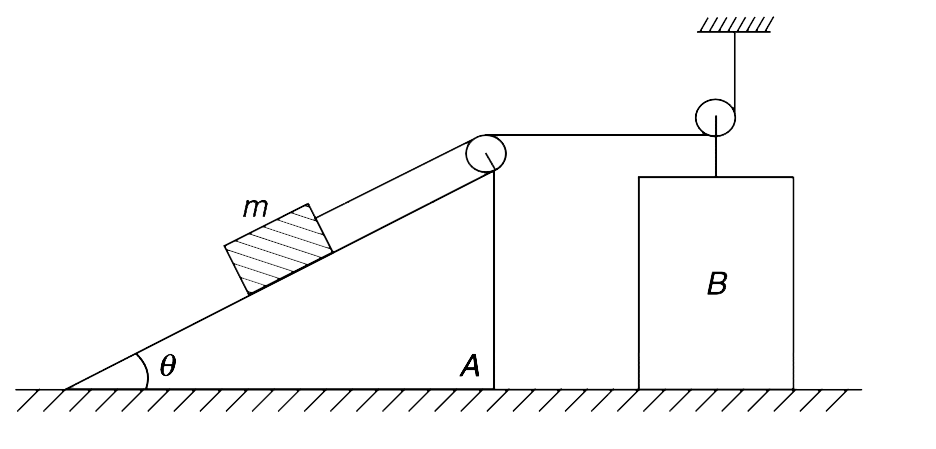 View Solution
View Solution