In the arrangement shown in figure mass of blocks A,B and C is 18.5kg.8kg and 1.5kg respectively . The bottom surface of A is A is smooth while coefficient of friction that between block A and C is μ1=1/3 between B and floor is μ2=1/5 System is relased from rest r=0 and pulley are light and friction Calculate acceleration of block A ,B and C

The correct Answer is:a=1ms−2,b=0.5ms−2c=3ms−2
Let the acceleration of A , B, and C are a,b, and c respectively
Net sum of charge of segment length in string should be zero
2(−xA)+2(−xB)+xc=0⇒c=2(a+b)

For A in vertical direction
N'=mAg+T+f1...(i)
where f1=μsN1=N13
In horizontal direction
2T−N1=mAa...(ii)
For C orizontal direction
N1=mca...(iii)
In vertical direction mcg−f1−T=mc2(a+b)...(iv)
mcg−N13−T=mc2(a+b)...(v)
For B: in vertical direction N''=mBg....(vi)
In horizontal direction
2T−f2=mBb
where f2=μ2N'=N'3....(vii)
After solving above equation we get
a=1ms−2,b=0.5ms−2
c=2(a+b)=2(1+0.5)=3ms−2
Net acceleration of c=√a2+c2=√12+32=√10ms−2
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 2Exercise:Single Correct
Explore 87 Videos
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 2Exercise:Multiple Correct
Explore 2 Videos
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 2Exercise:Exercise 7.3
Explore 27 Videos
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 1Exercise:Integer
Explore 5 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICS ENGLISHChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:INTEGER_TYPE
Explore 2 Videos
Similar Questions
Measles of A and B 10 kg and 5 kg respectively.y A is on smooth surface coefficient of friction between A and B is 0.4 if F=75N friction between the block is __ N.

View SolutionIn the arrangement shown in figure pulleys are mass of block A,b and C is m1=5kgm2=4kg and m3=2.5kg respectively .Co-efficient acceleration of friction for both the plane is μ=0.50 Calculate acceleration of which block when system is released from rest
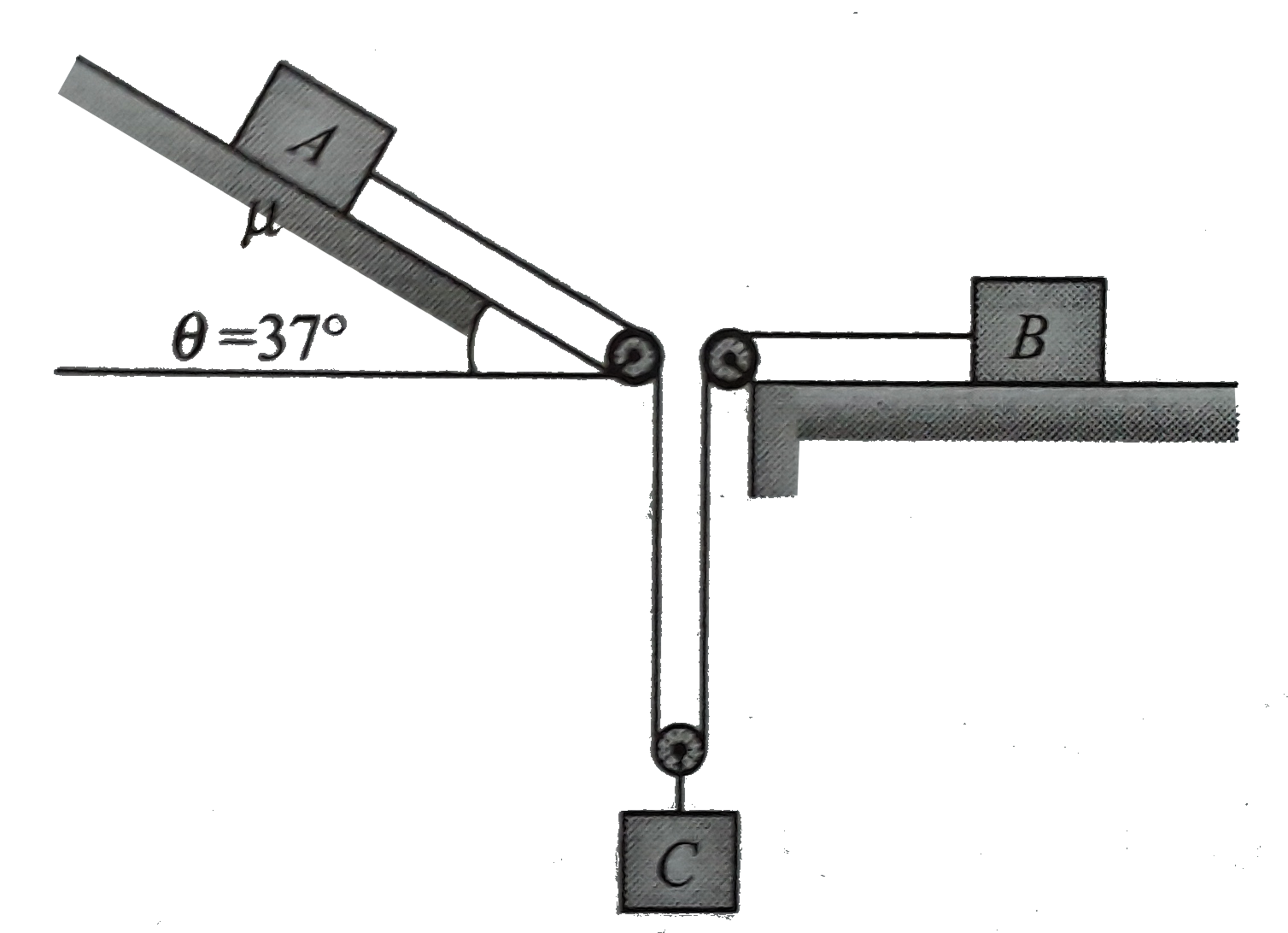
View SolutionIn the masses of A and B are 10 kg and 5 kg . Calculate the minimum mass of C which may stop A from slipping Coefficient of static friction between block A and table is 0.2
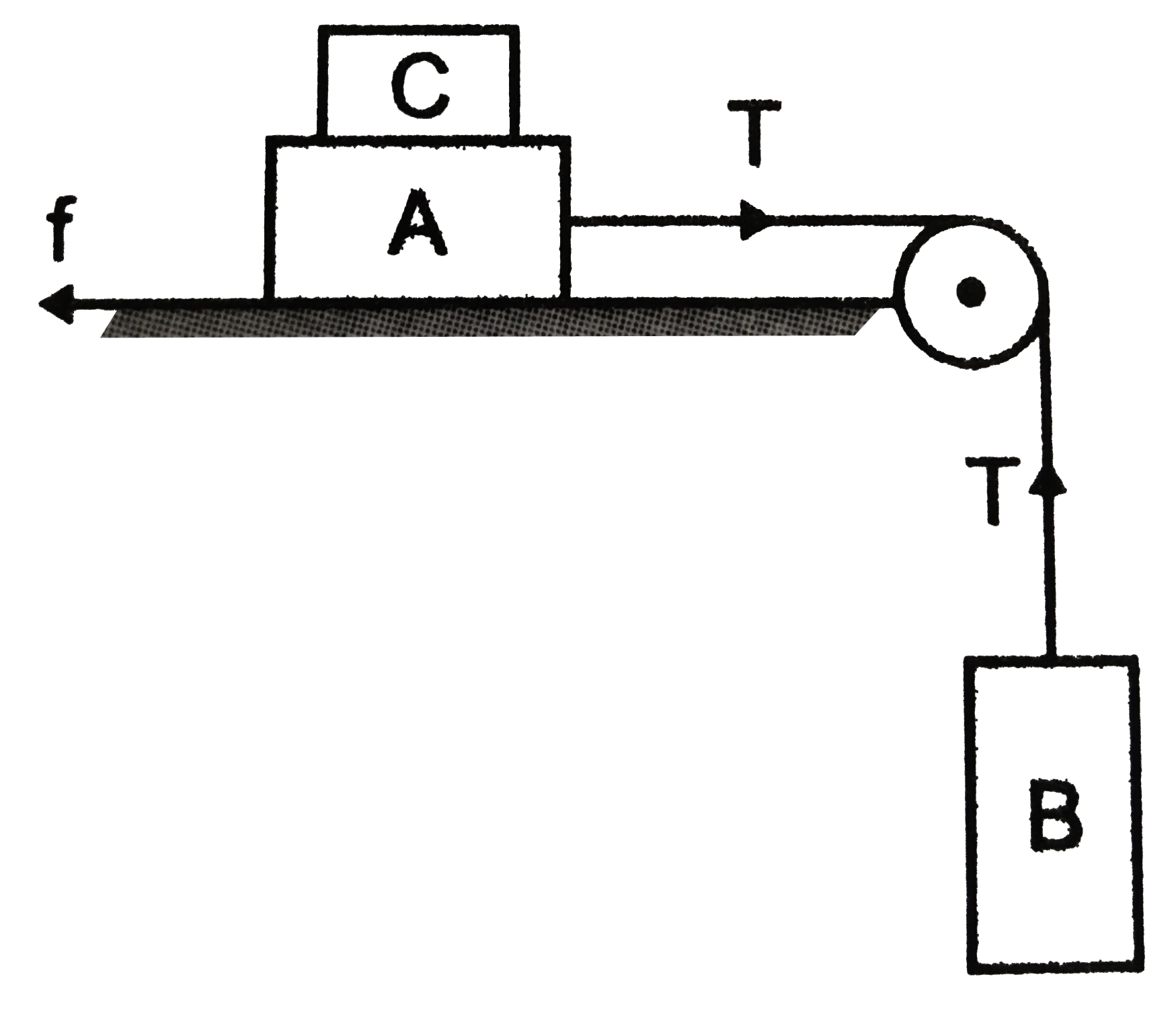 .
.
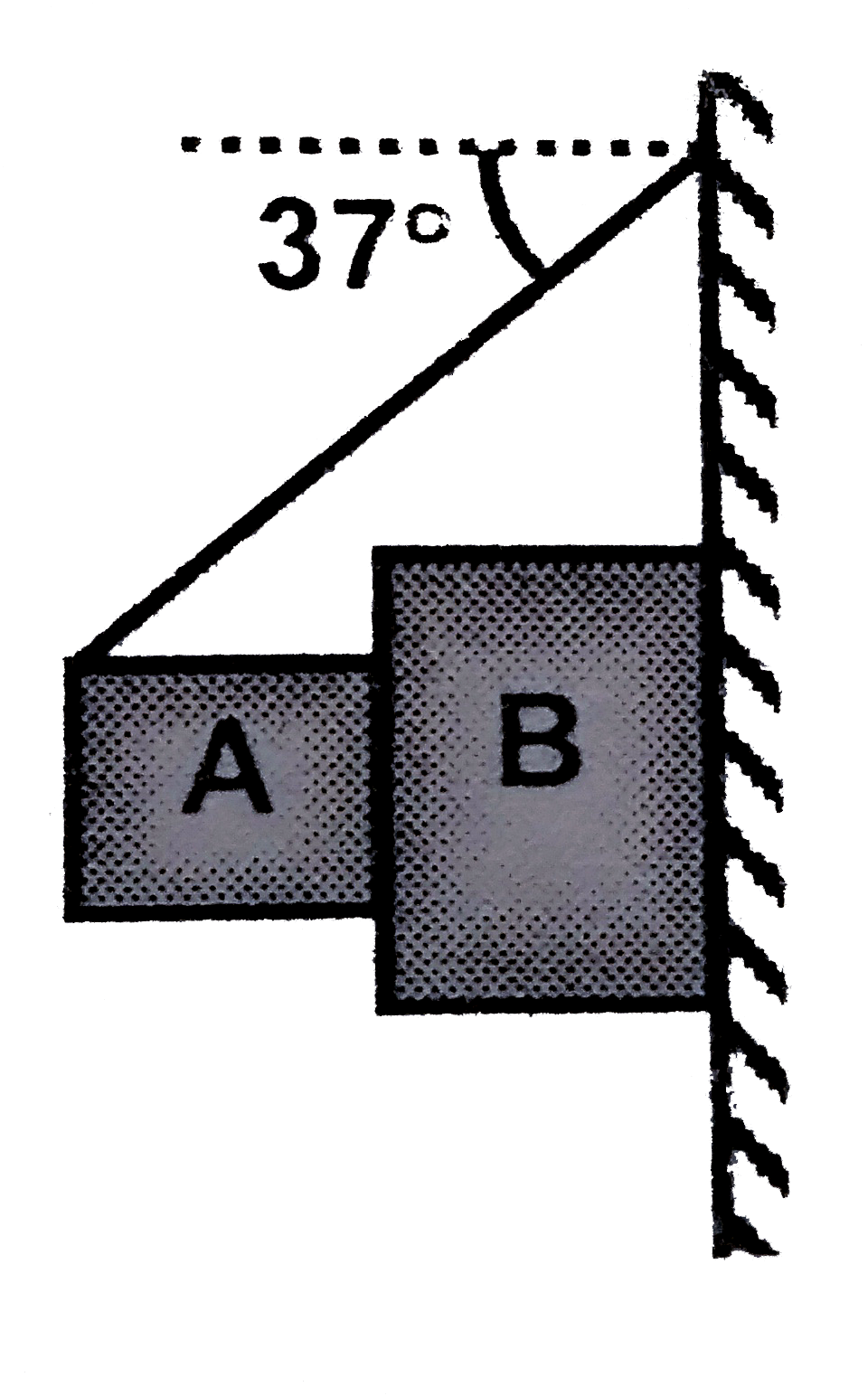
View SolutionTwo block A and B of mass 50kg and 300kg respectively are placed as shown in figure. Coefficient of friction between all surface is 12
Then (take g=10m/s)
View SolutionThe coefficient of friction between 4 kg and 5kg blocks is 0.2 and between 5kg block and grond is 0.1 respectively Choose the correct statements.

View SolutionBlock B rests on a smooth surface .The coefficient of static friction between A and B is μ=0.4 where F=30N then

Acceleration of upper block is
View SolutionBlock A and B of masses 5 kg and 10 kg are placed as shown in figure. If block A is pulled with 50 N. Find out acceleration of the A and B. If coefficient of friction between A and B is 0.5 and between B and ground is 0.4.

View SolutionBlocks A and B of masses 5 kg and 10kg are placed as shown in figure. If block A is pulled with 50 N. Find out acceleration of the A and B. if coefficient of friction between A and B is 0.5and between B and ground is 0.4.
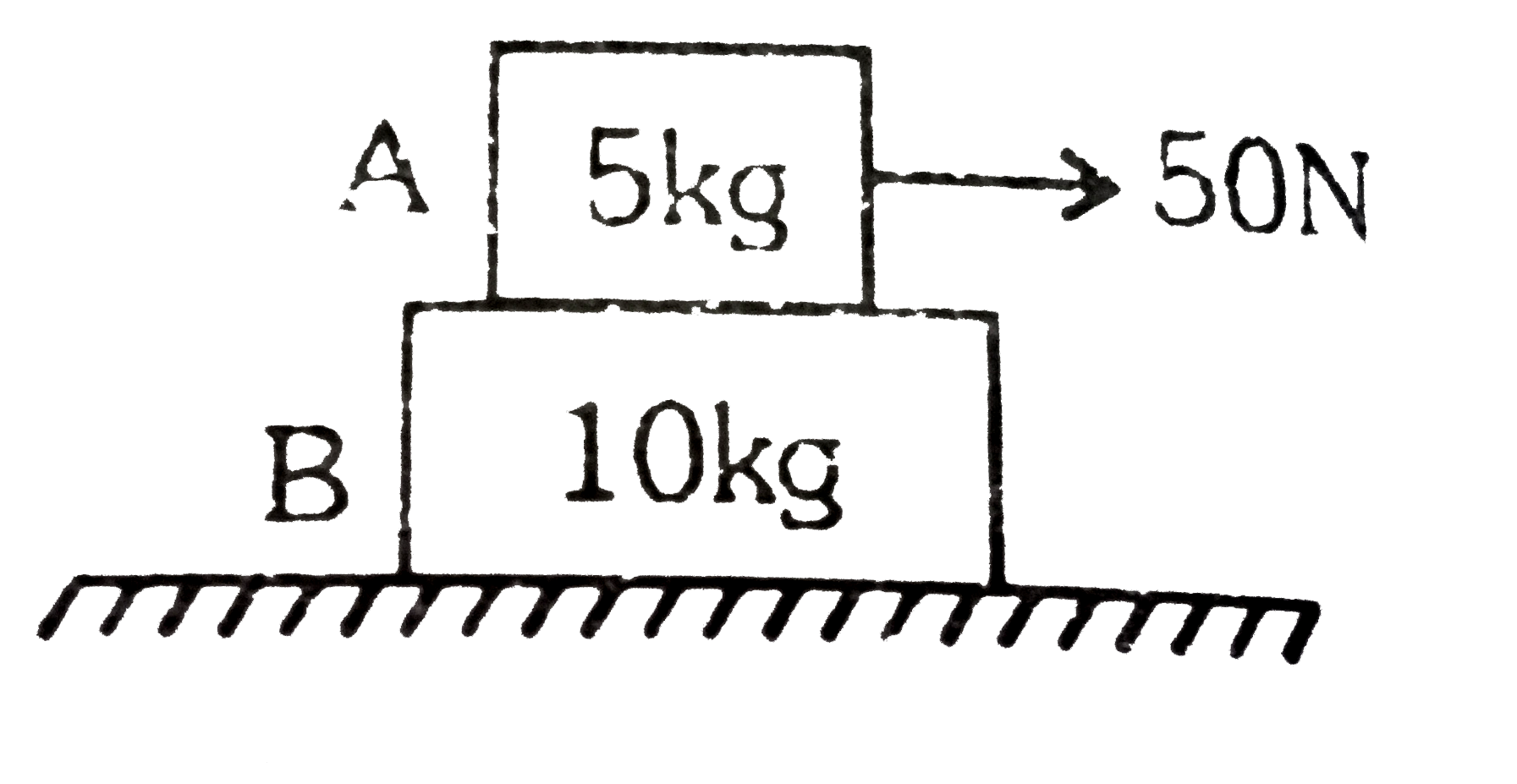
View SolutionThree blocks A , B and C of masses 4kg , 2kg and 1kg respectively are in contact on a frictionless surface, as shown. If a force of 14Nisappliedonthe4kgblock,thenthecontactforcebetweenAandB is.

View SolutionThree blocks A , B and C of masses 4kg , 2kg and 1kg respectively are in contact on a frictionless surface, as shown. If a force of 14Nisappliedonthe4kgblock,thenthecontactforcebetweenAandB is.

View Solution

