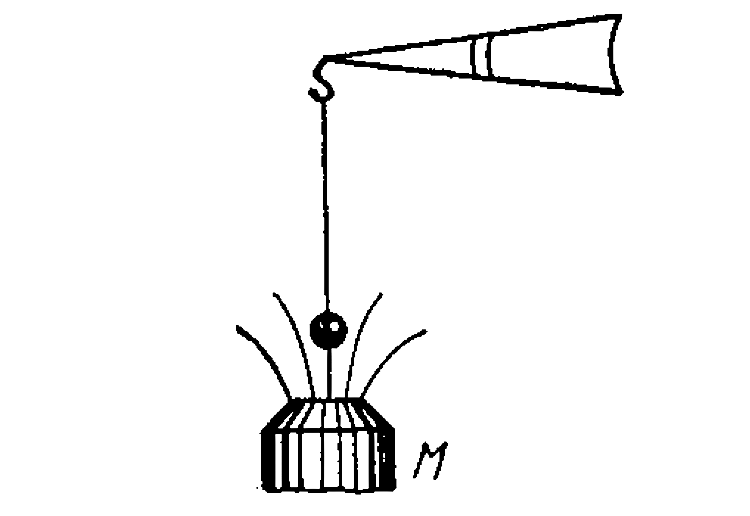
In the arrangement shown in Fig it is possible to measure (by means of a balance) the force with which a paramagnetic ball of volume V=41mm3 is attrated to a pole of the electromagnet M. The magnetic induction at the axis of the poleshoe depends on the height x as B=B0 exp (−ax2), where B0=1.50T,a=100m−2. Find:
(a) at what height xm the ball experiences the maximum attraction,
(b) the magnetic suspeptibility of the paranagnetic if the maximum attraction force equals Fmax=160μN.
Text Solution
The force is question is
→F=(−→Pm.→∇)→B=χBVμμ0dBdx
since B is essentially in the x-direction
So, Fx=χV2μ0dB2dx=χB20V2μ0ddx(e−2ax2)=−4axe−2ax2χB202μ0V
This is maximum when is derivative vanishes
i.e., 16a2x2−4a=0, or, xm=1√4a
The maximum force is,
Fmax=4a1√4ae−1/2χB20V2μ0=χB20Vμ0√ae
So, χ=(μ0Fmax√ea)/VB20=3.6×10−4
|
Updated on:21/07/2023
Related Playlists
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electromagnetic Induction84videos
ELECTRODYNAMICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Motion Of Charged Particle In Magnetic Field36videos
ELECTRODYNAMICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electric Current72videos
ELECTRODYNAMICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRICITY AND MAGNETISMEXERCISE - All Questions6videos
ELECTRICITY AND MAGNETISM
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTROMAGNETISMEXERCISE - All Questions24videos
ELECTROMAGNETISM
Similar Questions
Electromagnetic induction means
View SolutionElectromagnetic induction means
View SolutionElectromagnetic induction means -
View SolutionThe magnetic induction B and the force F on a pole m are related by
View SolutionElectromagnetic induction means ……………….
View SolutionFor the arrangement shown in Fig. determine the magnetic field at centre O.
 View Solution
View SolutionFor the arrangement shown in Fig. determine the magnetic field at centre O.
 View Solution
View SolutionFor the arrangment as shown in the figure, the magnetic induction at the centre is
 View Solution
View SolutionIn an electromagnetic wave, the direction of the magnetic field induction →B is-
View SolutionFor a paramagnetic material,the dependence of the magnetic susceptibility x on the absolute temprature T is given by
View Solution

