Gauss's law and Coulomb's law , although expressed in different forms , are equivalent ways of describing the relation between charge and electric field in static conditions . Gauss's law is ε0ϕ=qencl,when q(encl) is the net charge inside an imaginary closed surface called Gaussian surface. The two equations hold only when the net charge is in vaccum or air .
The net flux of the electric field through the surface due to q3 and q4 is
zero
positive
negative
cannot say
The correct Answer is:A
To solve the problem, we need to apply Gauss's law, which relates the electric flux through a closed surface to the charge enclosed by that surface. Here’s a step-by-step solution:
Step 1: Understand Gauss's Law
Gauss's law states that the electric flux (Φ) through a closed surface is proportional to the charge (q_encl) enclosed within that surface. Mathematically, it is expressed as:
Φ=qenclϵ0
where ϵ0 is the permittivity of free space.
Step 2: Identify the Charges
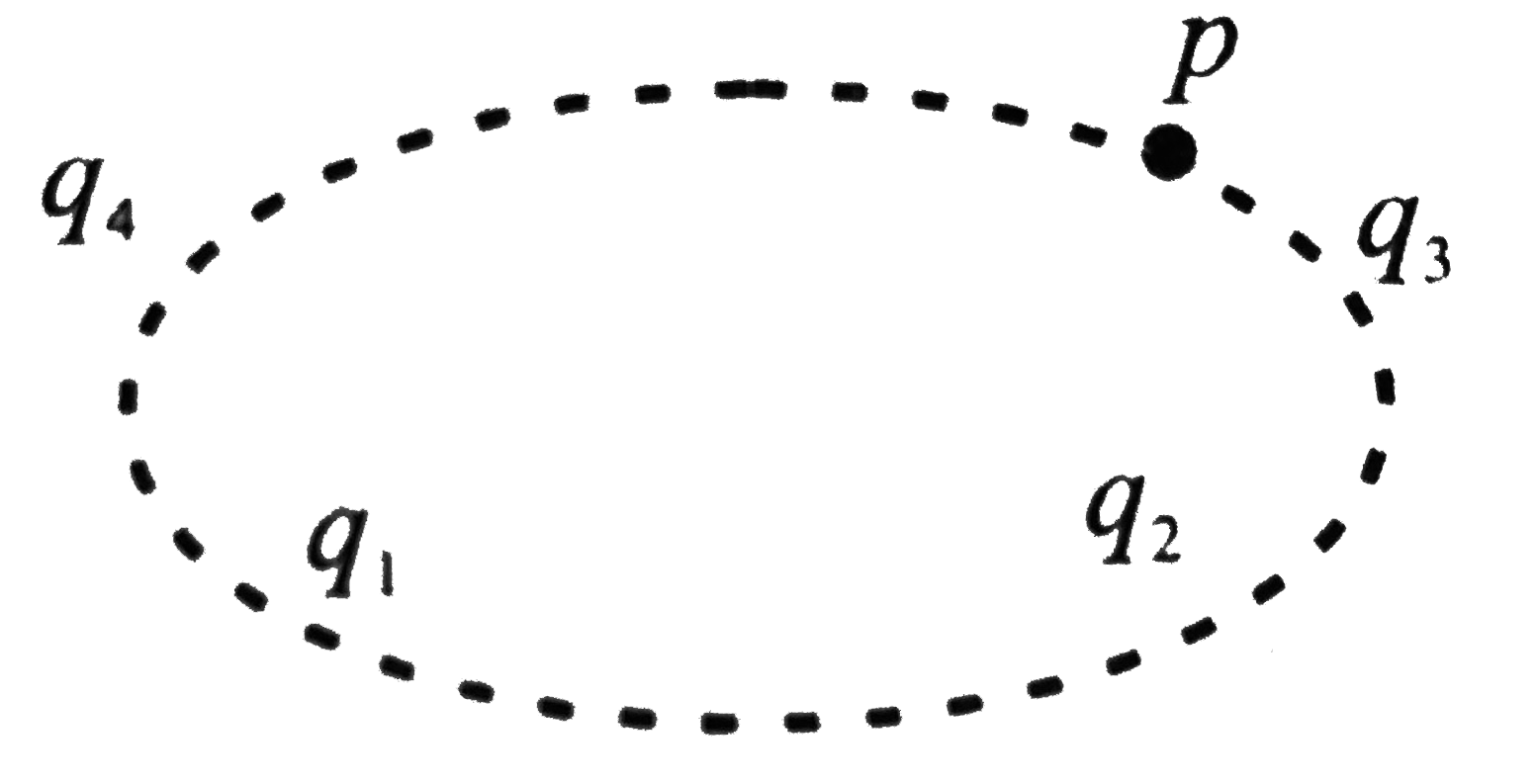
In the given scenario, we have charges q3 and q4 which are located outside the Gaussian surface, while charges q1 and q2 are inside the Gaussian surface.
Step 3: Determine the Enclosed Charge
Since q3 and q4 are outside the Gaussian surface, they do not contribute to the enclosed charge. Therefore, the total enclosed charge qencl is solely due to q1 and q2.
Step 4: Calculate the Electric Flux Due to q3 and q4
According to Gauss's law, since q3 and q4 are outside the Gaussian surface, their contribution to the electric flux through the surface is zero. Thus:
Φq3,q4=0
Step 5: Conclusion
The net electric flux through the Gaussian surface due to charges q3 and q4 is zero because they are not enclosed by the surface.
Final Answer
The net flux of the electric field through the surface due to q3 and q4 is:
Φ=0
---
Gauss's law states that the electric flux (Φ) through a closed surface is proportional to the charge (q_encl) enclosed within that surface. Mathematically, it is expressed as:
Φ=qenclϵ0
where ϵ0 is the permittivity of free space.
In the given scenario, we have charges q3 and q4 which are located outside the Gaussian surface, while charges q1 and q2 are inside the Gaussian surface.
Since q3 and q4 are outside the Gaussian surface, they do not contribute to the enclosed charge. Therefore, the total enclosed charge qencl is solely due to q1 and q2.
According to Gauss's law, since q3 and q4 are outside the Gaussian surface, their contribution to the electric flux through the surface is zero. Thus:
Φq3,q4=0
The net electric flux through the Gaussian surface due to charges q3 and q4 is zero because they are not enclosed by the surface.
The net flux of the electric field through the surface due to q3 and q4 is:
Φ=0
Topper's Solved these Questions
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRIC FLUX AND GAUSS LAWExercise:Subjective type
Explore 7 Videos
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRIC FLUX AND GAUSS LAWExercise:MCQ s
Explore 38 Videos
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRIC FLUX AND GAUSS LAWExercise:Multiple Correct
Explore 8 Videos
- ELECTRIC CURRENT AND CIRCUITBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRIC CURRENT AND CIRCUITExercise:Interger
Explore 8 Videos
- ELECTRIC POTENTIALBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRIC POTENTIALExercise:DPP 3.5
Explore 15 Videos
Similar Questions
Gauss's law and Coulomb's law , although expressed in different forms , are equivalent ways of describing the relation between charge and electric field in static conditions . Gauss's law is ε0ϕ=qencl,when q(encl) is the net charge inside an imaginary closed surface called Gaussian surface. The two equations hold only when the net charge is in vaccum or air .
A Gaussian surface encloses two of the four positively charged particles. The particles that contribute to the electric field at a point P on the surface are
View SolutionGauss's law and Coulomb's law , although expressed in different forms , are equivalent ways of describing the relation between charge and electric field in static conditions . Gauss's law is ε0ϕ=qencl,when q(encl) is the net charge inside an imaginary closed surface called Gaussian surface. The two equations hold only when the net charge is in vaccum or air .
If the charge q3 and q4 are displaced (always remaining outside the Gaussian surface), then consider the following two statements :
A: Electric field at each point on the Gaussian surface will remain same .
B: The value of ∮→E.d→A for the Gaussian surface will remain same.
View Solution
Knowledge Check
The surface considered for Gauss's law is called
AClosed surfaceBSphereical surfaceCGaussian surfaceDPlane surfaceA point charge 4μC is at the centre of a cubic Gaussian surface 10 cm on edge. Net electric flux through the surface is
A2.5×105Nm2C−1B4.5×105Nm2C−1C4.5×106Nm2C−1D2.5×106Nm2C−1
Net charge on an electric dipole is ………….. .
View SolutionConsider the charge configuration and a spherical Gaussian surface as shown in the figure. When calculating the flux of the electric field over the spherical surface, the electric field will be due to.
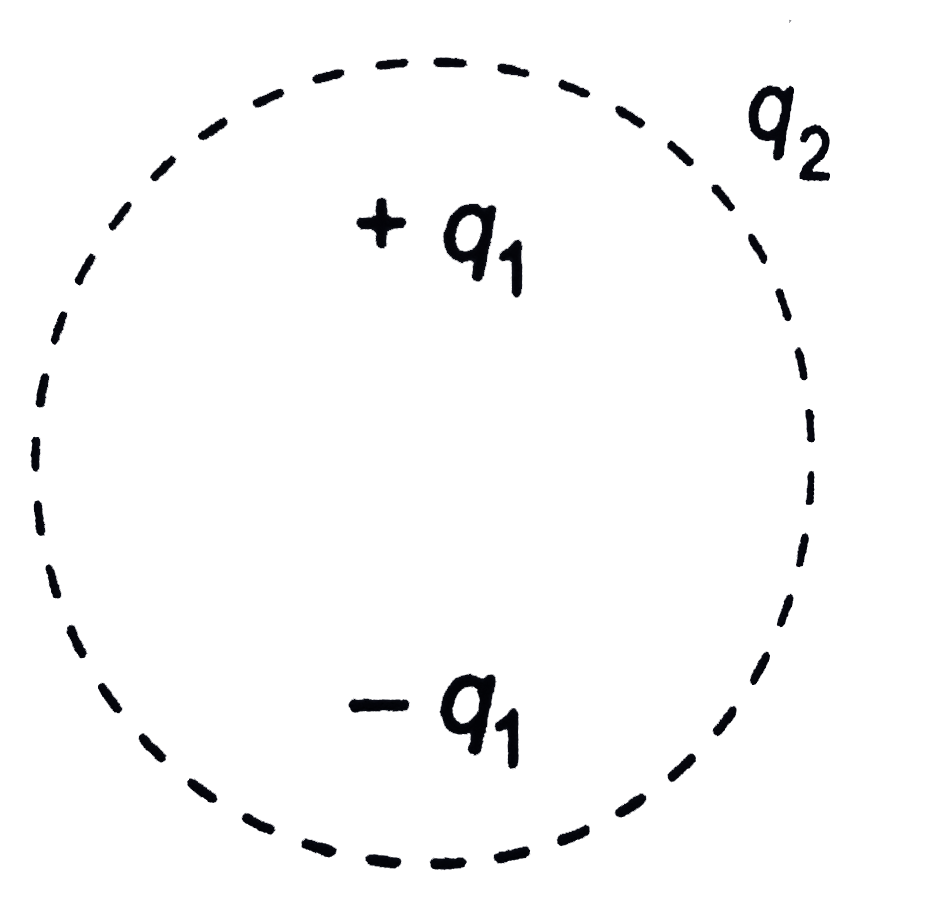
View SolutionConsider the charge configuration and a spherical Gaussian surface as shown in the figure. When calculating the flux of the electric field over the spherical surface, the electric field will be due to.

View SolutionIn Gauss's law ε0∮→E.¯¯¯¯ds=Qenclosed, is →E only due to charges enclosed ?
View SolutionFigure shows four charges q1,q2,q3,andq4 fixed is space. Then the total flux of the electric field through a closed surface S, due to all the charges, is

View SolutionA charge Q is enclosed by a Gaussian surface. If surface area is doubled and charge Q is tripled then the outward electric flux will
View Solution

