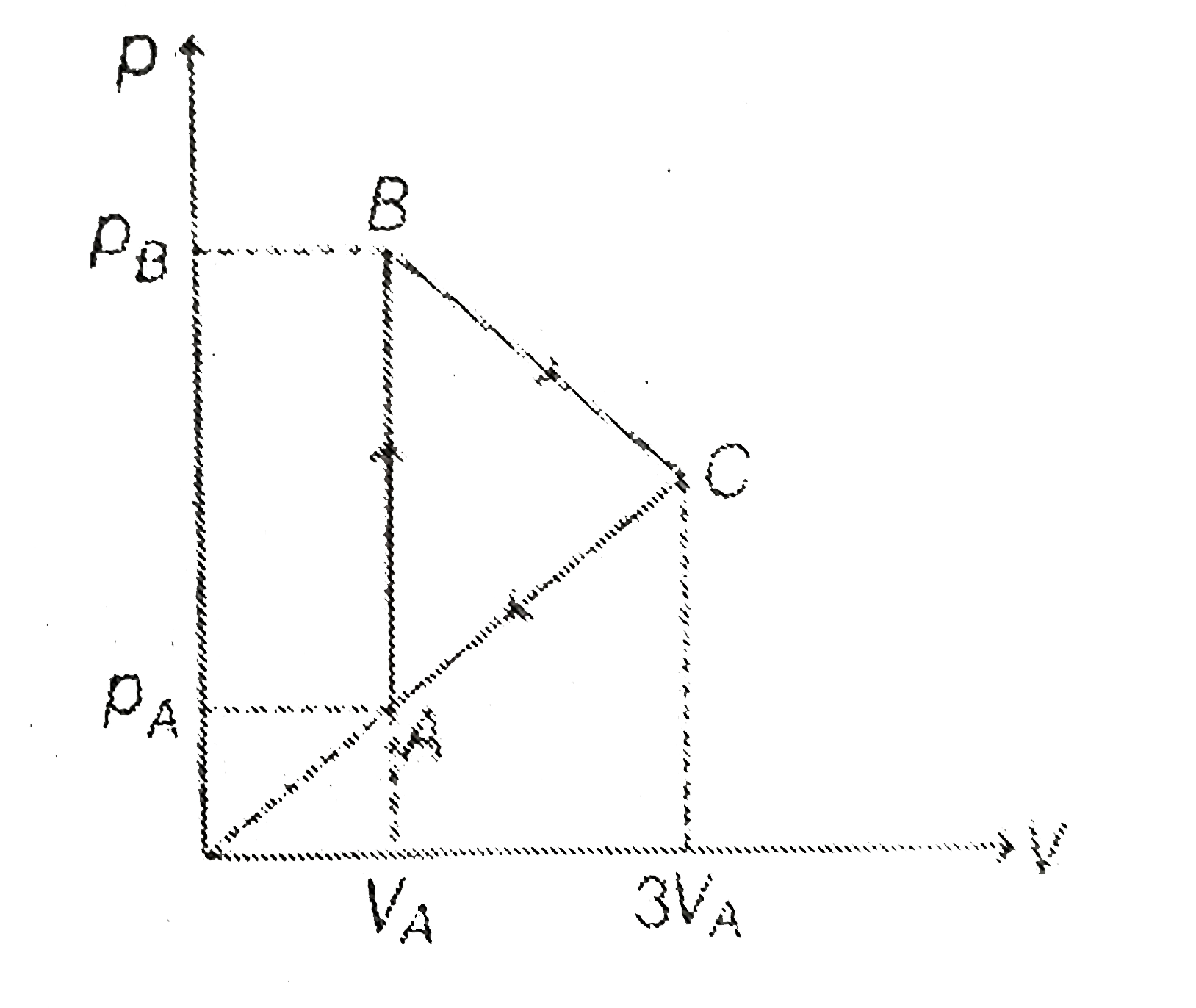
Four moles of an ideal gas is initially in a state A having pressure 2×105N/m2 and temperature 200 K . Keeping pressure constant the gas is taken to state B at temperature of 400K. The gas is then taken to a state C in such a way that its temperature increases and volume decreases. Also from B to C, the magnitude of dTdV increases. The volume of gas at state C is eaual to its volume at state A. Now gas is taken is initial state A keeping volume constant. A total of 1000 J heat is rejected from the sample in the cyclic process. Take R=8.3J/K/mol.
The work done by the gas along path B to C is
1000J
−1000J
−7640J
5640J
The correct Answer is:C
To solve the problem, we will follow these steps:
Step 1: Understand the Process
We have an ideal gas undergoing a cyclic process:
- From state A to B (constant pressure, temperature increases from 200 K to 400 K).
- From state B to C (temperature increases, volume decreases).
- From state C back to A (volume constant).
Step 2: Calculate Work Done in Each Segment
1. From A to B:
- Since the pressure is constant, the work done (W_AB) can be calculated using the formula:
WAB=PΔV
- We need to find the change in volume (ΔV). We can use the ideal gas law:
PV=nRT
- At state A:
VA=nRTAP=4×8.3×2002×105=66402×105=0.0332m3
- At state B (T_B = 400 K):
VB=nRTBP=4×8.3×4002×105=132802×105=0.0664m3
- Thus, the change in volume from A to B is:
ΔVAB=VB−VA=0.0664−0.0332=0.0332m3
- Work done from A to B:
WAB=PΔVAB=2×105×0.0332=6640J
2. From B to C:
- We know that the total work done in the cyclic process is zero (since it returns to the initial state), and the heat rejected is -1000 J. Thus:
Qtotal=WAB+WBC+WAC=0
- Rearranging gives us:
WBC=−1000−WAB−WAC
- Since W_AC is zero (volume is constant), we have:
WBC=−1000−6640=−7640J
Step 3: Conclusion
The work done by the gas along the path B to C is:
WBC=−7640J
We have an ideal gas undergoing a cyclic process:
- From state A to B (constant pressure, temperature increases from 200 K to 400 K).
- From state B to C (temperature increases, volume decreases).
- From state C back to A (volume constant).
1. From A to B:
- Since the pressure is constant, the work done (W_AB) can be calculated using the formula:
WAB=PΔV
- We need to find the change in volume (ΔV). We can use the ideal gas law:
PV=nRT
- At state A:
VA=nRTAP=4×8.3×2002×105=66402×105=0.0332m3
- At state B (T_B = 400 K):
VB=nRTBP=4×8.3×4002×105=132802×105=0.0664m3
- Thus, the change in volume from A to B is:
ΔVAB=VB−VA=0.0664−0.0332=0.0332m3
- Work done from A to B:
WAB=PΔVAB=2×105×0.0332=6640J
- We know that the total work done in the cyclic process is zero (since it returns to the initial state), and the heat rejected is -1000 J. Thus:
Qtotal=WAB+WBC+WAC=0
- Rearranging gives us:
WBC=−1000−WAB−WAC
- Since W_AC is zero (volume is constant), we have:
WBC=−1000−6640=−7640J
The work done by the gas along the path B to C is:
WBC=−7640J
Topper's Solved these Questions
Similar Questions
Four moles of an ideal gas is initially in a state A having pressure 2×105N/m2 and temperature 200 K . Keeping pressure constant the gas is taken to state B at temperature of 400K. The gas is then taken to a state C in such a way that its temperature increases and volume decreases. Also from B to C, the magnitude of dTdV increases. The volume of gas at state C is eaual to its volume at state A. Now gas is taken is initial state A keeping volume constant. A total of 1000 J heat is rejected from the sample in the cyclic process. Take R=8.3J/K/mol.
Which graph between temperture T and volume V for the cyclic process is correct.
View SolutionFour moles of an ideal gas is initially in state A having pressure 2×105N/m2 and temperature 200K . Keeping the pressure constant the gas is taken to state B at temperature of 400K. The gas is then taken to a state C in such a way that its temperature increases and volume decreases. Also from B to C , the magnitude of dT/dV increases. The volume of gas at state C is equal to its volume at state A. Now gas is taken to initial state A keeping volume constant. A total 1000J of heat is withdrawn from the sample of the cyclic process . Take R=8.3J/K/mol. The volume of gas at state C is
View Solution
Knowledge Check
What is the effect on the pressure of a gas if its temperature is increased at constant volume ?
AThe pressure of the gas increases.BThe pressure of the gas decreases .CThe pressure of the gas remains same .DThe pressure of the gas becomes half.
One mole of an ideal monoatomic gas is taken at a temperature of 300K. Its volume is doubled keeping its pressure constant. Find the change in internal energy.
View SolutionCan the temperature of a gas increased keeping its pressure and volume constant ?
View SolutionThe temperature of a given mass of a gas is increased from 19∘C to 20∘C at constant pressure. The volume V of the gas is
View SolutionA sample of ideal gas is taken through the cyclic process shown in the figure. The temerauture of the gas in state A is TA =200 K. In states B and C the temperature of the gas is the same.
Net work done by the gas in the process is
View SolutionAt constant pressure, the ratio of increases in volume of an ideal gas per degree rise in kelvin temperature to its volume is
View SolutionFour moles of an ideal gas at a pressure of 4 atm and at a temperature of 70∘C expands is othermally to four times its initial volume : What is (i) the final temperature and (ii) the final volume ?
View SolutionA vessel is filled with an ideal gas at a pressure of 20atm and is a temperature of 27∘C One - half of the mass is removed from the vessel and the temperature of the remaining gas is increased to 87∘C. At this temperature, Find the pressure of the gas.
View Solution

