Find the potential energy of a system of four particles each of mass 2m kept at the vertices of a square of side x. Also find the potential at the centr of the square.
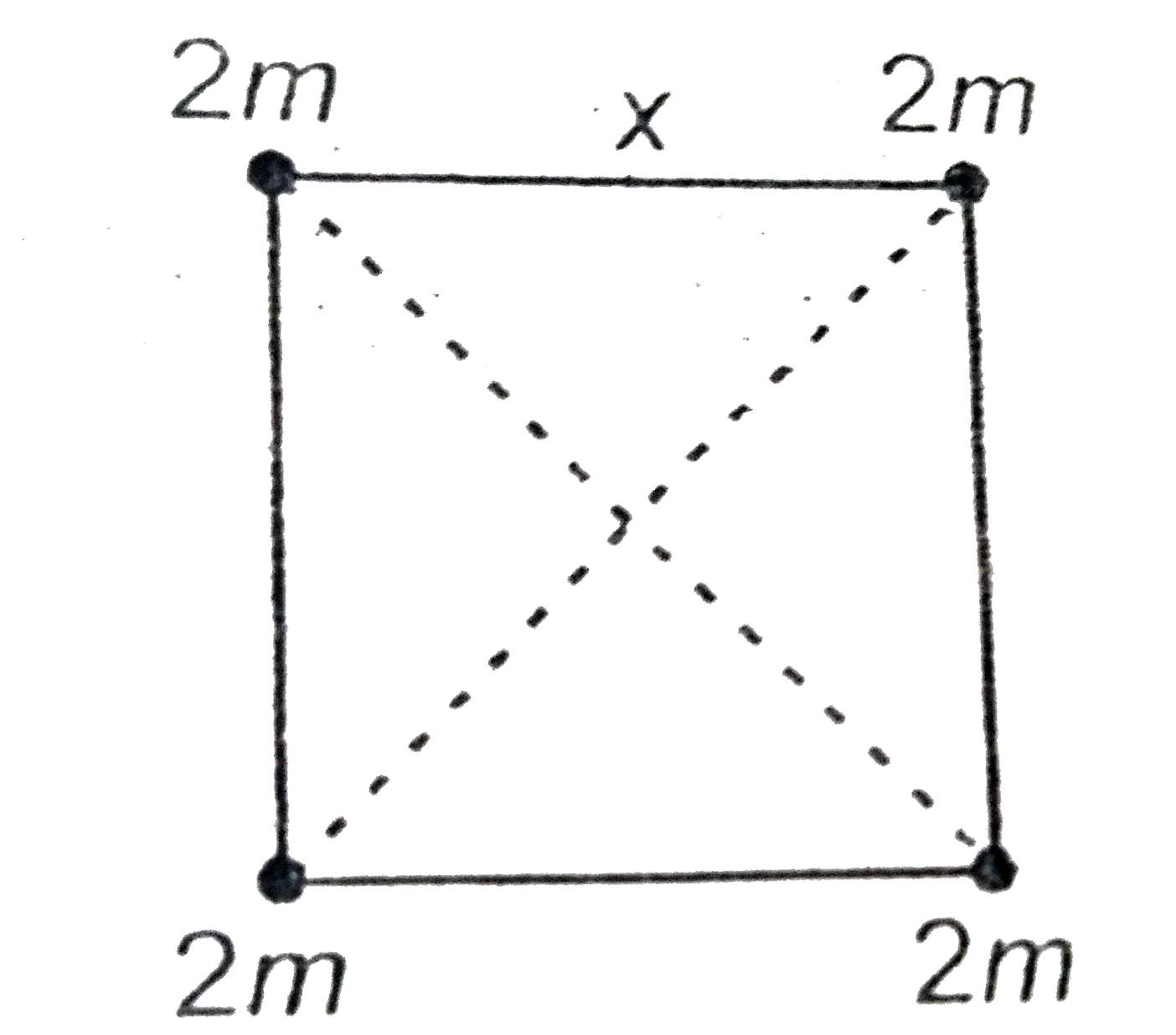
Distance of diagonal pair is =√x2+x2=√2x
Now, potential energy of system = potential enegy of pairs of mass at the ends of the sides + potential energy of masses at diagonal ends
=4[−G(2m)2x]+2[−G(2m)2√2x]
=−16Gm2x−8Gm2√2x
=−21.64Gm2x
Now, the gravitational potential at the centre will be V(centre) =4⎡⎢
⎢⎣−G(2m)(√2x2)⎤⎥
⎥⎦=8√2Gmx
Related Playlists
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - Try Yourself33videos
GRAVITATION
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION -A (Objective Type Questions (one option is correct))50videos
GRAVITATION
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - D9videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions10videos
KINETIC THEORY
Similar Questions
Four particles each of mass m are placed at the vertices of a square of side l. the potential at the centre of square is
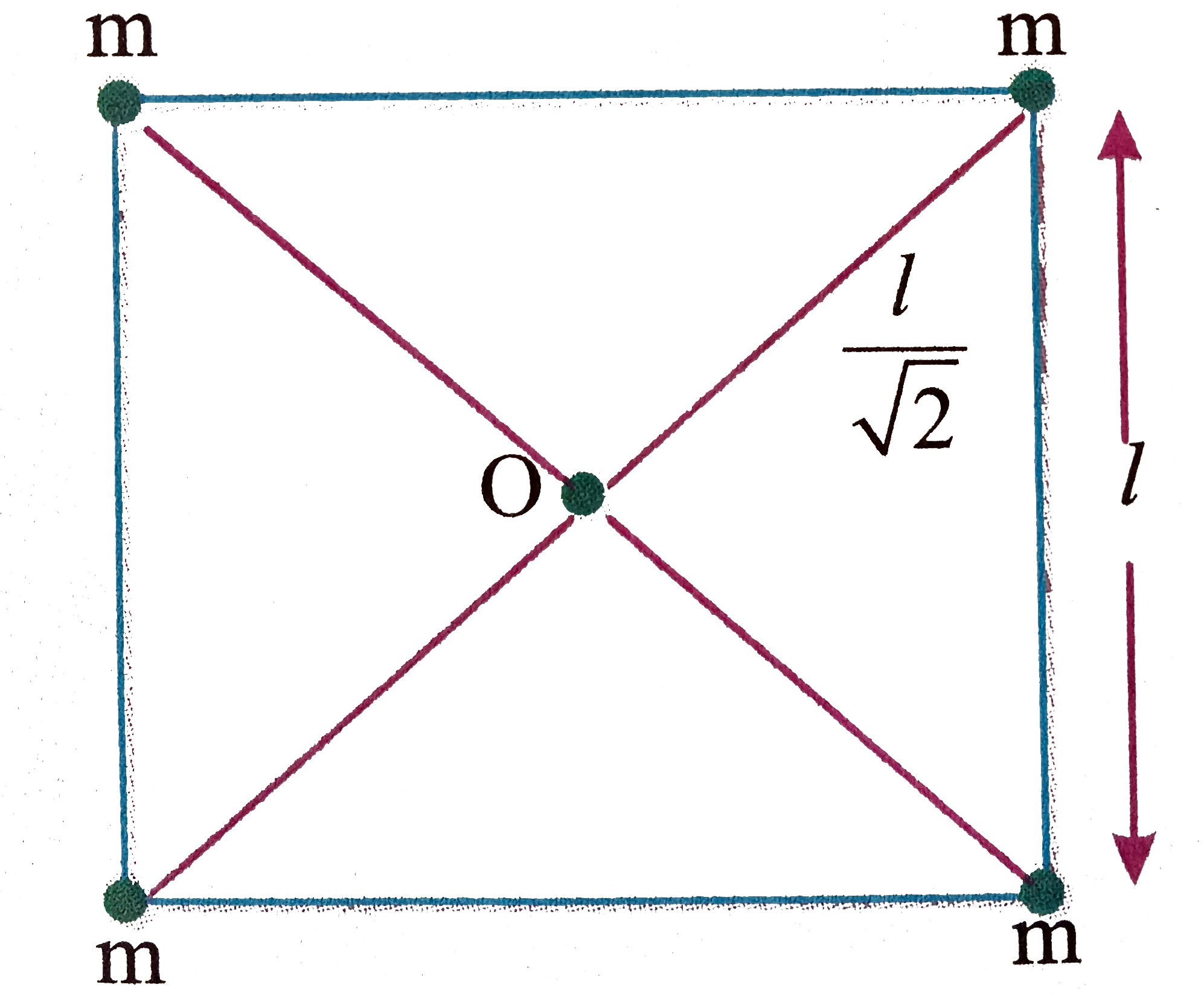
View SolutionFind the gravitational potential energy of a system of four particles, each of mass m placed at the verticles of a square of side l. Also obtain the gravitaitonal potential at centre of the square.
 View Solution
View SolutionFind the potential energy of a system of 3 particles kept at the vertices of an equilateral triangle of side r.
View SolutionFind the potential energy of 4-particles, each of mass 1 kg placed at the four vertices of a square of side length 1 m.
View SolutionFour particles each of mass m are kept at the four vertices of a square of side 'a' . Find gravitational potential energy of this system.
View SolutionFind the electric potential energy of the system of charges
View SolutionFind the potential energy of a system of eight particles of mass M placed at the vertices of a cube of side L. neglect the self energy of the particles.
View SolutionFour point charges are placed at the corners of a square of side l. Calculate potential at the centre of square.
 View Solution
View SolutionThe gravitational potential energy of a system of three particles of mass m each kept at the vertices of equilateral triangle of side x will be
View SolutionFour particles each of mass 'm' are placed at the four vertices of a square 'a' .Find net force on any one the particle.
View Solution



