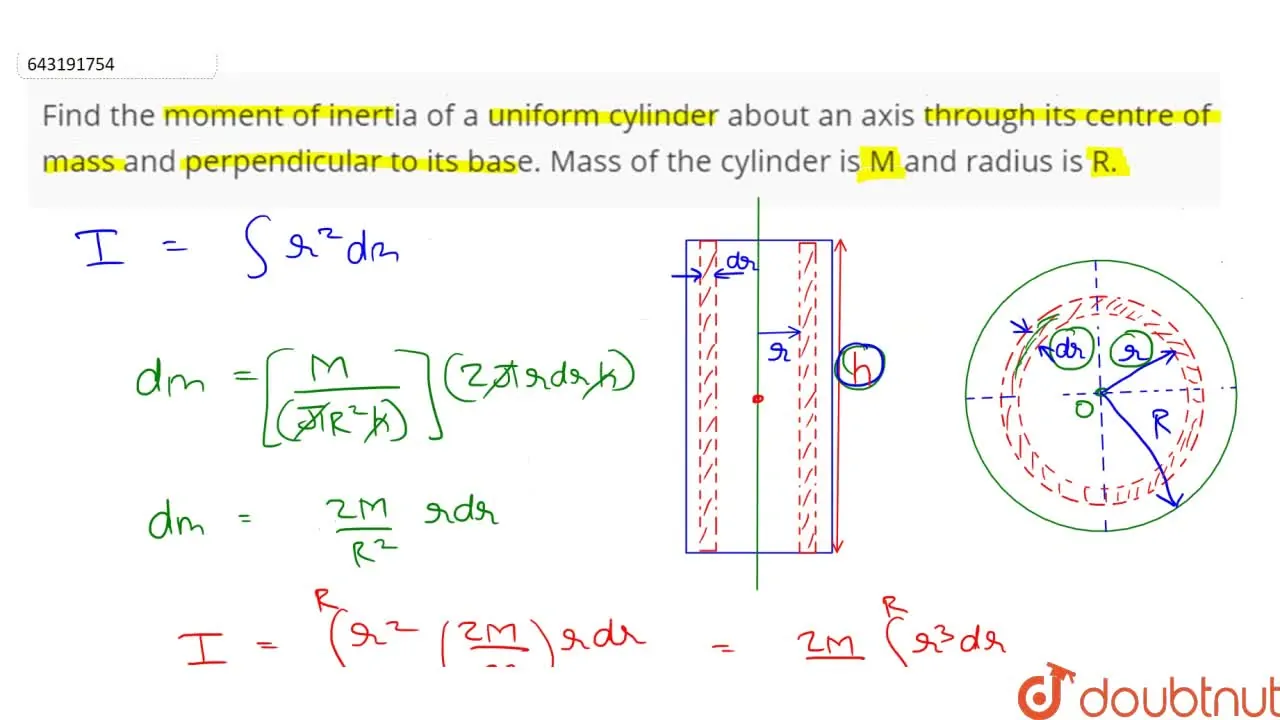
Find the moment of inertia of a uniform cylinder about an axis through its centre of mass and perpendicular to its base. Mass of the cylinder is M and radius is R.
The cylinder can be divided into annular shells of width dr and length l as shown in figure
The moment of inertia of one of thee shells
I=∫r2dm=r3(ρdV)
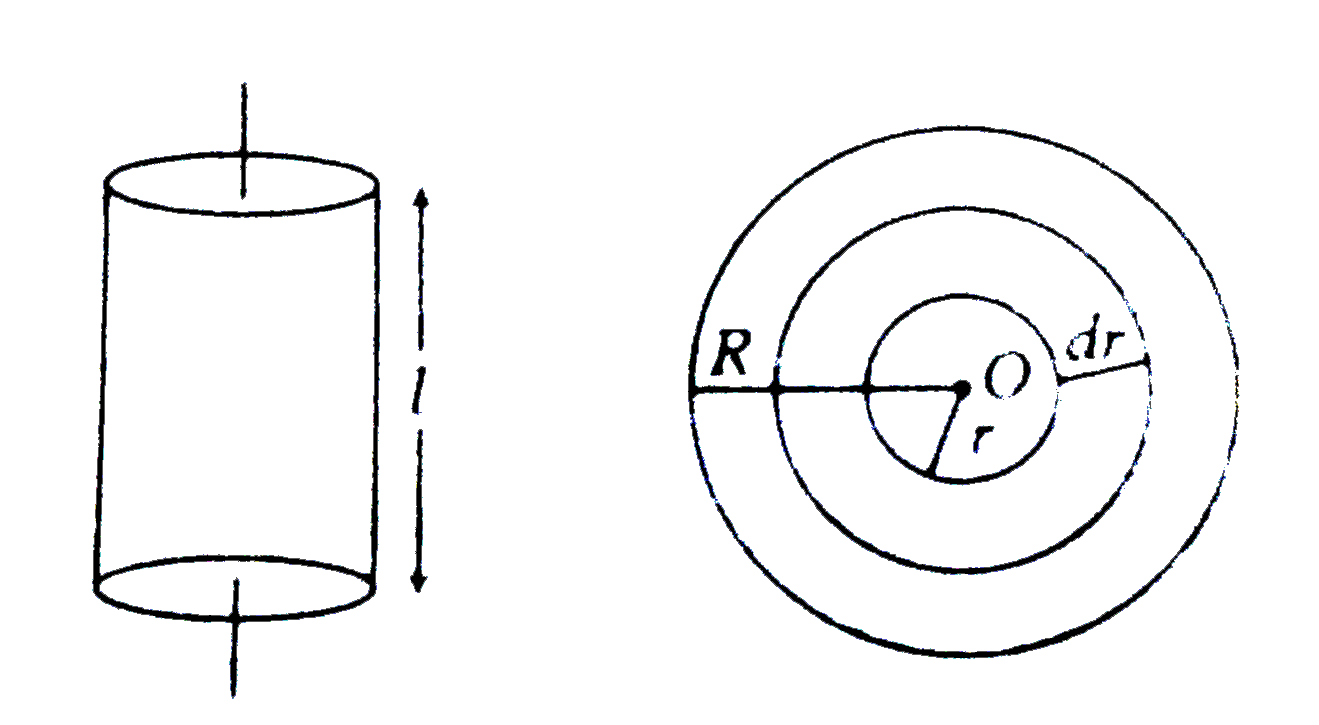
Here, ρ= density, dV =volume of shell =2πrldr
∴I=2πρlr3dr
They cylinder's moment of inertia is found by integrating this expression between O and R
So, I=2πρl∫R0r3dr=πρl2R4...(i)
The density ρ of the cylinder is the mass divided by the volume
∴ρ=MπR2l....(ii)
From Eqs. (i) and (ii), we have
I=12MR2.
Related Playlists
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - Check point 9.120videos
ROTATION
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - Check point 9.220videos
ROTATION
- BOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.14videos
RAY OPTICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions2videos
ROTATIONAL MECHANICS
Similar Questions
The moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
View SolutionMoment of inertia of a uniform quarter disc of radius R and mass M about an axis through its centre of mass and perpendicular to its plane is :
View SolutionMoment of inertia of a uniform quarter disc of radius R and mass M about an axis through its centre of mass and perpendicular to its plane is :
View SolutionThe moment of inertia of a uniform semicircular wire of mass m and radius r, about an axis passing through its centre of mass and perpendicular to its plane is mr2(−kπ2). Find the value of k.
View SolutionThe moment of inertia of a uniform semicircular wire of mass M and radius R about an axis passing through its centre of mass and perpendicular to its plane is xMR210. Find the value of x? (Take π2=10)
View SolutionThe moment of inertia of a solid cylinder of mass M, length 2R and radius R about an axis passing through the centre of mass and perpendicular to the axis of the cylinder is I1 and about an axis passing through one end of the cylinder and perpendicular to the axis of cylinder is I2
View SolutionMoment of inertia of a cylinder of mass M, length L and radius R about an axis passing through its centre and perpendicular to the axis of the cylinder is I=M(R24+L212). If such a cylinder is to be made for a given mass of a material, the ratio L/R for it to have minimum possible I is :
View SolutionFind the moment of inertia of a circular disk or solid cylinder of radius R about the axis through the centre and perpendicular to the flat surface.
 View Solution
View SolutionMoment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
View SolutionThe moment of inertia of a solid cylinder about its own axis is the same as its moment of inertia about an axis passing through its centre of gravity and perpendicular to its length. The relation between its length L and radius R is :
View Solution