Find the moment of inertia of a cylinder of mass M, radius R and length L about an axis passing through its centre and perpendicular to its symmetry axis. Do this by integrating an elemental disc along the length of the cylinder.
To find the moment of inertia of a cylinder of mass M, radius R, and length L about an axis passing through its center and perpendicular to its symmetry axis, we will use the method of integration by considering elemental discs along the length of the cylinder.
1. Visualize the Cylinder:
- Imagine a cylinder of radius R and length L. The axis of rotation is perpendicular to the symmetry axis and passes through the center of the cylinder.
2. Elemental Disk:
- Consider an elemental disk of thickness dx located at a distance x from the center of the cylinder. The radius of this disk is R.
3. Moment of Inertia of the Disk:
- The moment of inertia dI of this elemental disk about the axis passing through its center is given by:
dI=12dm⋅R2
- Here, dm is the mass of the elemental disk.
4. Finding dm:
- The mass per unit length of the cylinder is:
ML
- Therefore, the mass of the elemental disk dm can be expressed as:
dm=ML⋅dx
5. Substituting dm into the Moment of Inertia:
- Substitute dm into the expression for dI:
dI=12(ML⋅dx)R2
- This simplifies to:
dI=MR22Ldx
6. Integrating Along the Length of the Cylinder:
- To find the total moment of inertia I, integrate dI from −L2 to L2:
I=∫L2−L2dI=∫L2−L2MR22Ldx
7. Evaluating the Integral:
- The integral evaluates to:
I=MR22L(x)L2−L2=MR22L(L2−(−L2))=MR22L⋅L=MR22
8. Final Result:
- The moment of inertia of the cylinder about the specified axis is:
I=12MR2
- Imagine a cylinder of radius R and length L. The axis of rotation is perpendicular to the symmetry axis and passes through the center of the cylinder.
- Consider an elemental disk of thickness dx located at a distance x from the center of the cylinder. The radius of this disk is R.
- The moment of inertia dI of this elemental disk about the axis passing through its center is given by:
dI=12dm⋅R2
- Here, dm is the mass of the elemental disk.
- The mass per unit length of the cylinder is:
ML
- Therefore, the mass of the elemental disk dm can be expressed as:
dm=ML⋅dx
- Substitute dm into the expression for dI:
dI=12(ML⋅dx)R2
- This simplifies to:
dI=MR22Ldx
- To find the total moment of inertia I, integrate dI from −L2 to L2:
I=∫L2−L2dI=∫L2−L2MR22Ldx
- The integral evaluates to:
I=MR22L(x)L2−L2=MR22L(L2−(−L2))=MR22L⋅L=MR22
- The moment of inertia of the cylinder about the specified axis is:
I=12MR2
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICS ENGLISHChapter:RIGID BODY DYNAMICS 1Exercise:Exercise 2.3
Explore 15 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICS ENGLISHChapter:RIGID BODY DYNAMICS 1Exercise:Exercise 2.4
Explore 11 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICS ENGLISHChapter:RIGID BODY DYNAMICS 1Exercise:Exercise 2.1
Explore 6 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICS ENGLISHChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:INTEGER_TYPE
Explore 2 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICS ENGLISHChapter:RIGID BODY DYNAMICS 2Exercise:Interger
Explore 2 Videos
Similar Questions
The moment of inertia of a cube of mass M and edge length a about an axis passing through one of its edge is
View SolutionMoment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
View SolutionCalculate the moment of inertia of a ring of mass 2kg and radius 2cm about an axis passing through its centre and perpendicular to its surface.
View SolutionCalculate the moment of inertia of a ring of mass 2kg and radius 2cm about an axis passing through its centre and perpendicular to its surface.
View SolutionFind the moment of inertia of a uniform square plate of mass M and edge of length 'l' about its axis passing through P and perpendicular to it.

View SolutionMoment of inertia of a thin rod of mass m and length l about an axis passing through a point l/4 from one end and perpendicular to the rod is
View SolutionThe moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
View Solutionfind the radius of gyration of a rod of mass m and length 2l about an axis passing through one of its ends and perpendicular to its length.
View SolutionThe moment of inertia of a solid cylinder of mass M, length 2R and radius R about an axis passing through the centre of mass and perpendicular to the axis of the cylinder is I1 and about an axis passing through one end of the cylinder and perpendicular to the axis of cylinder is I2
View SolutionMatch the Moment of inertia of a solid cylinder of mass m, radius R and length l along various axis as shown in figure.
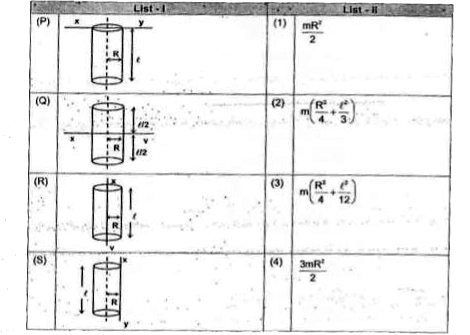
View Solution

