Find the moment of inertia of a cylinder of mass $M$ , radius $R$ and length $L$ about an axis passing through its centre and perpendicular to its symmetry axis. Do this by integrating an elemental disc along the length of the cylinder.

Video Solution

Text Solution

Verified by Experts

Moment of inertia of $n$ elemental disc at the distance $x$ from axis $1$
$d m = \frac{M d x}{L}$

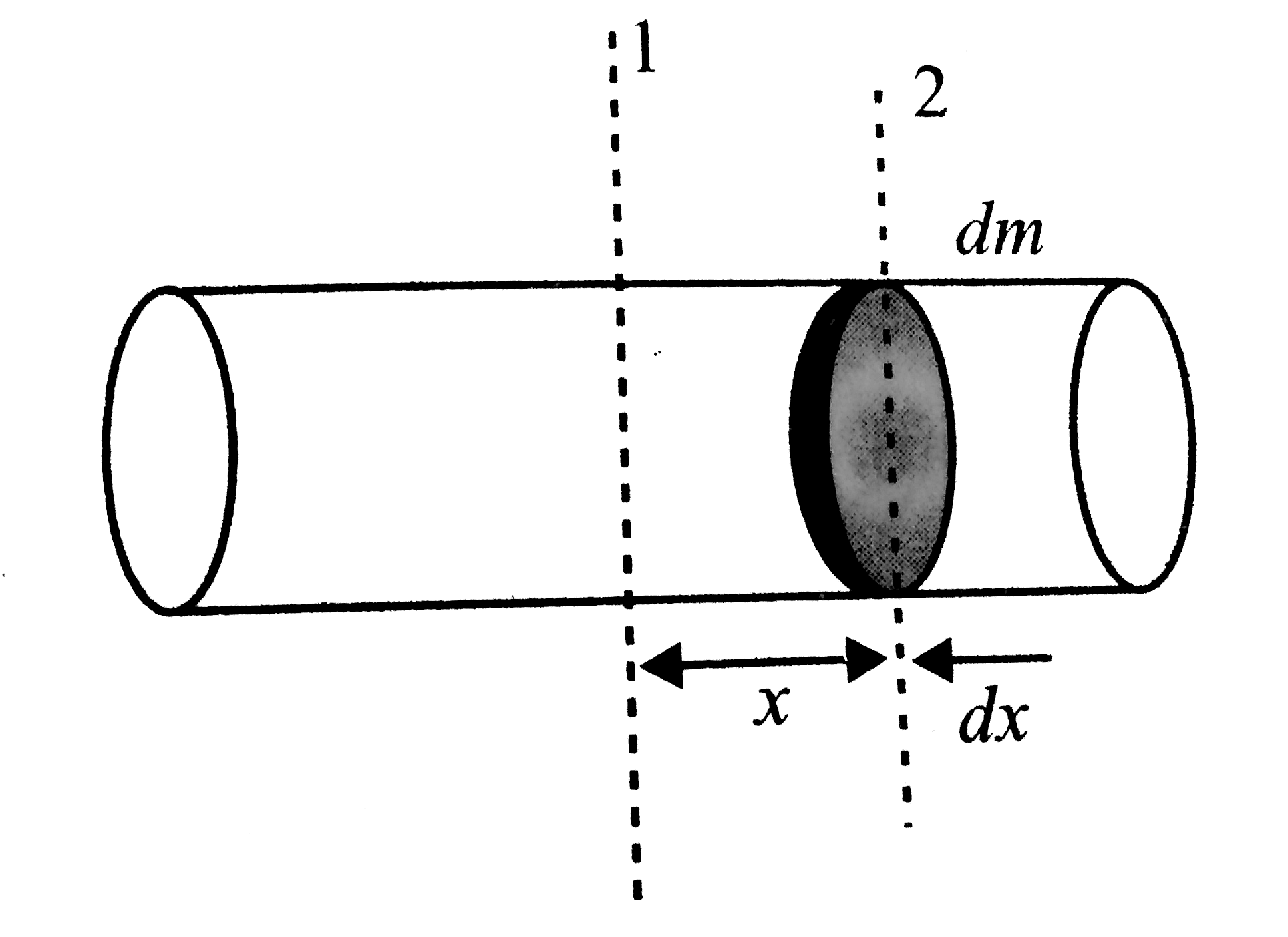
$M I$ of the element disc about axis $1$
$I_{1} = \int_{L / 2} (\frac{d m}{2} R^{2} + d m x^{2})$
$= \int_{- L / 2}^{L / 2} \frac{M}{2 L} R^{3} d x + \int_{- L / 2}^{L / 2} \frac{M}{L} x^{2} d x$
$= \frac{M R^{2}}{2} + \frac{M L^{2}}{12}$

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Moment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
A $1 / 2 M R^{2}$
B $M R^{2}$
C $1 / 4 M R^{2}$
D $3 / 4 M R^{2}$
Question 2 - Select One
The moment of inertia of a cylinder of radius R, length L and mass M about an axis passing through its centre of mass and normal to its length is
A $\frac{M L^{2}}{12}$
B $\frac{M R^{2}}{4}$
C $M [\frac{L^{2}}{12} + \frac{R^{2}}{4}]$
D $M [\frac{L^{2}}{12} + \frac{R^{2}}{2}]$
Question 3 - Select One
Moment of inertia of a solid cylinder of length L and diameter D about an axis passing through its centre of gravity and perpendicular to its geometric axis is
A $M (\frac{D^{2}}{4} + \frac{L^{2}}{12})$
B $M (\frac{L^{2}}{16} + \frac{D^{2}}{8})$
C $M (\frac{D^{2}}{4} + \frac{L^{2}}{6})$
D $M (\frac{L^{2}}{12} + \frac{D^{2}}{16})$

CENGAGE PHYSICS-RIGID BODY DYNAMICS 1-Exercise 2.2

Home
Ask Doubt
Profile