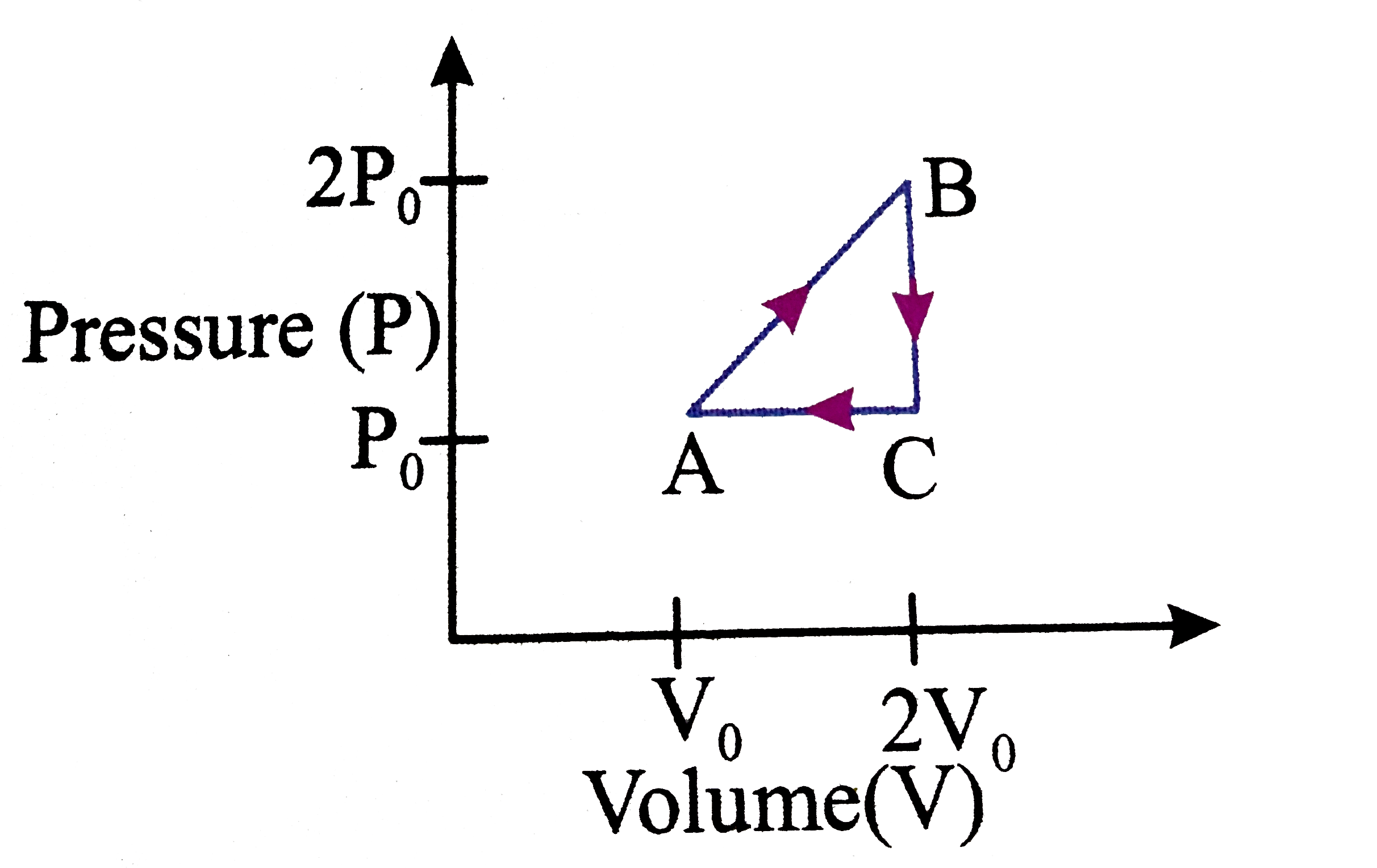Find the efficiency of the thermodynamics cycle shown in figure for an ideal diatomic gas.
Text Solution
Let n be the number of moles of the gas and the temperature be T0 in the state A.
Now, work done during the cycle
W=12×(2V0−V0)(2P0−P0)=12P0V0
For the heat (ΔQ1) given during the process
A→B, we have ΔQ1=ΔWAB+ΔUAB
ΔWAB=area under the straight line AB
=12(P0+2P0)(2V0−V0)=3P0V02
Applying equation of state for the gas in the state A&B.
P0V0T0=(2P0)(2V0)TB⇒TB=4T0
∴UAB=nCvΔT=n[5R2](4T0−T0)=15nRT02=15P0V02
∴ΔQ1=32P0V0+152P0V0=9P0V0
Obviously, the processes. B→CandC→A involve the abstraction of heat from the gas.
Efficiency=Work done per cycleTotal heat supplie per cycle
i.e., η=12P0V09P0V0=118
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - THERMODYNAMICSEXERCISE - EXERCISE - 1A135videos
THERMODYNAMICS
- BOOK - AAKASH SERIESCHAPTER - THERMODYNAMICSEXERCISE - EXERCISE - 1B32videos
THERMODYNAMICS
- BOOK - AAKASH SERIESCHAPTER - THERMODYNAMICSEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS7videos
THERMODYNAMICS
- BOOK - AAKASH SERIESCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II) PRACTICE SHEET (ADVANCED) Integer/Subjective Type Questions2videos
THERMAL PROPERTIES OF MATTER
- BOOK - AAKASH SERIESCHAPTER - THERMOMETRY EXERCISE - Numerical Exercise (LEVEL- 1)11videos
THERMOMETRY
Similar Questions
Knowledge Check
- Question 1 - Select One
During the thermodynamic process shown in figure for an ideal gas
 AΔT=0BΔQ=0CW<0DΔU>0
AΔT=0BΔQ=0CW<0DΔU>0 - Question 2 - Select One
The efficiency of the reversible cycle shown in the figure will be
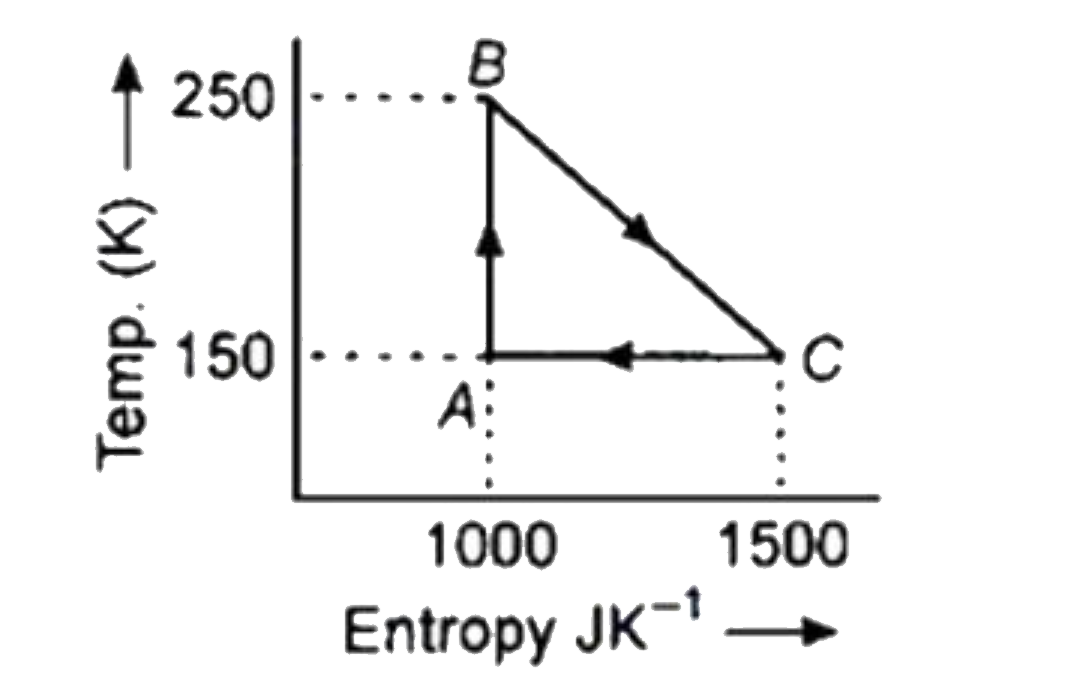 A33.33%B56%C66%D25%
A33.33%B56%C66%D25% - Question 3 - Select One
The efficiency of the reversible cycle shown in the given figure is
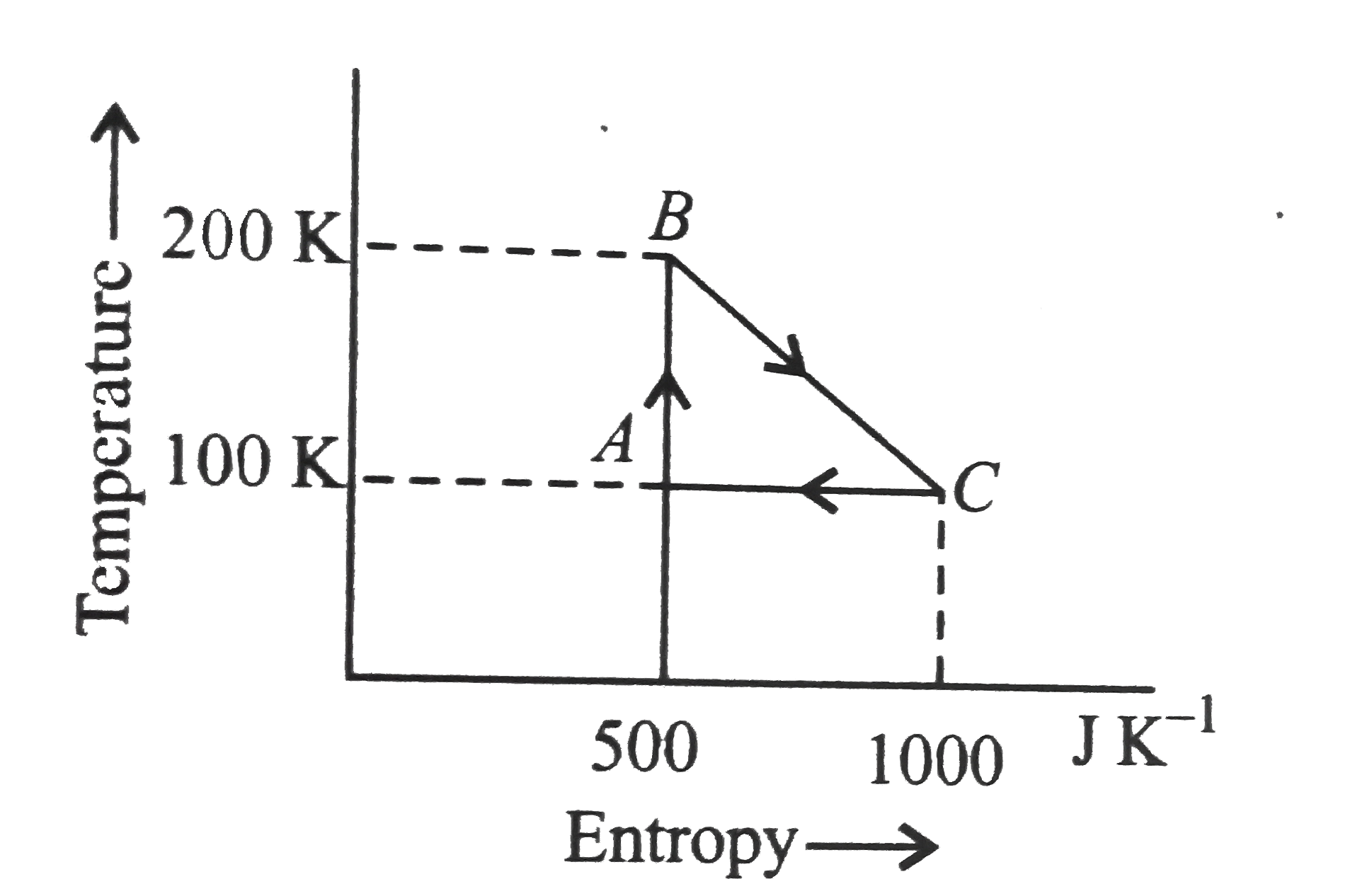 A33.33%B56%C66%D16.7%
A33.33%B56%C66%D16.7%
The efficiency of the reversible cycle shown in the figure will be
 View Solution
View SolutionThe efficiency of the reversible cycle shown in the given figure is
 View Solution
View SolutionFor the thermodynamic cycle shown in figure find (a) net output work of the gas during the cycle, (b) net heat flow into the gas per cycle.
 View Solution
View SolutionFor the thermodynamic cycle shown in figure find (a) net output work of the gas during the cycle, (b) net heat flow into the gas per cycle.
 View Solution
View Solution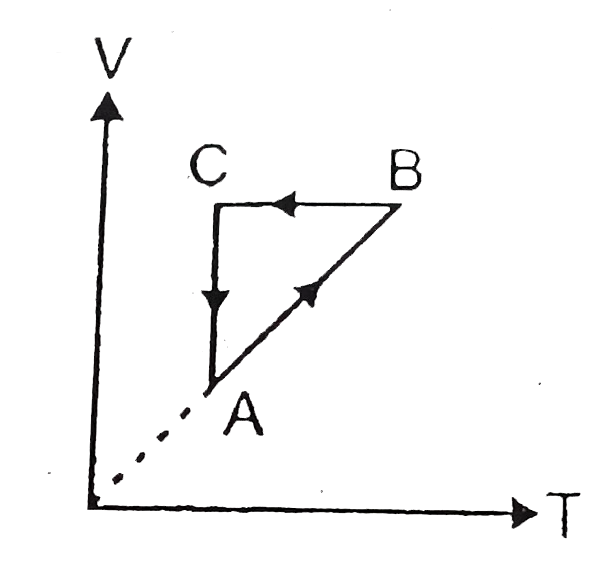
An ideal undergoes a thermodynamic cycle as shown in figure. Which of the following graphs represent the same cycle?View Solution