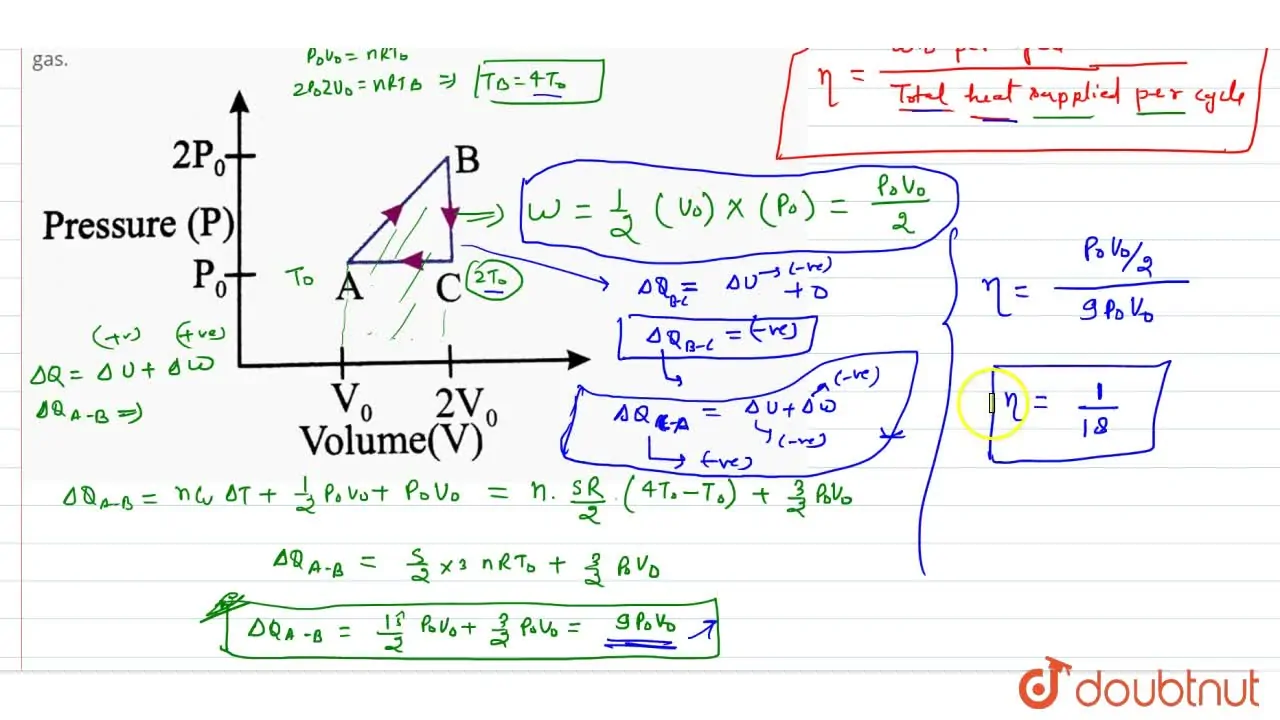
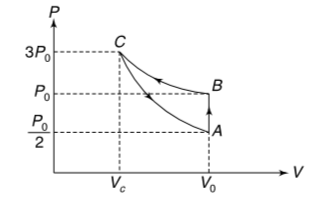
Find the efficeincy of the thermodynamic cycle shown in figure for an ideal diatomic gas.
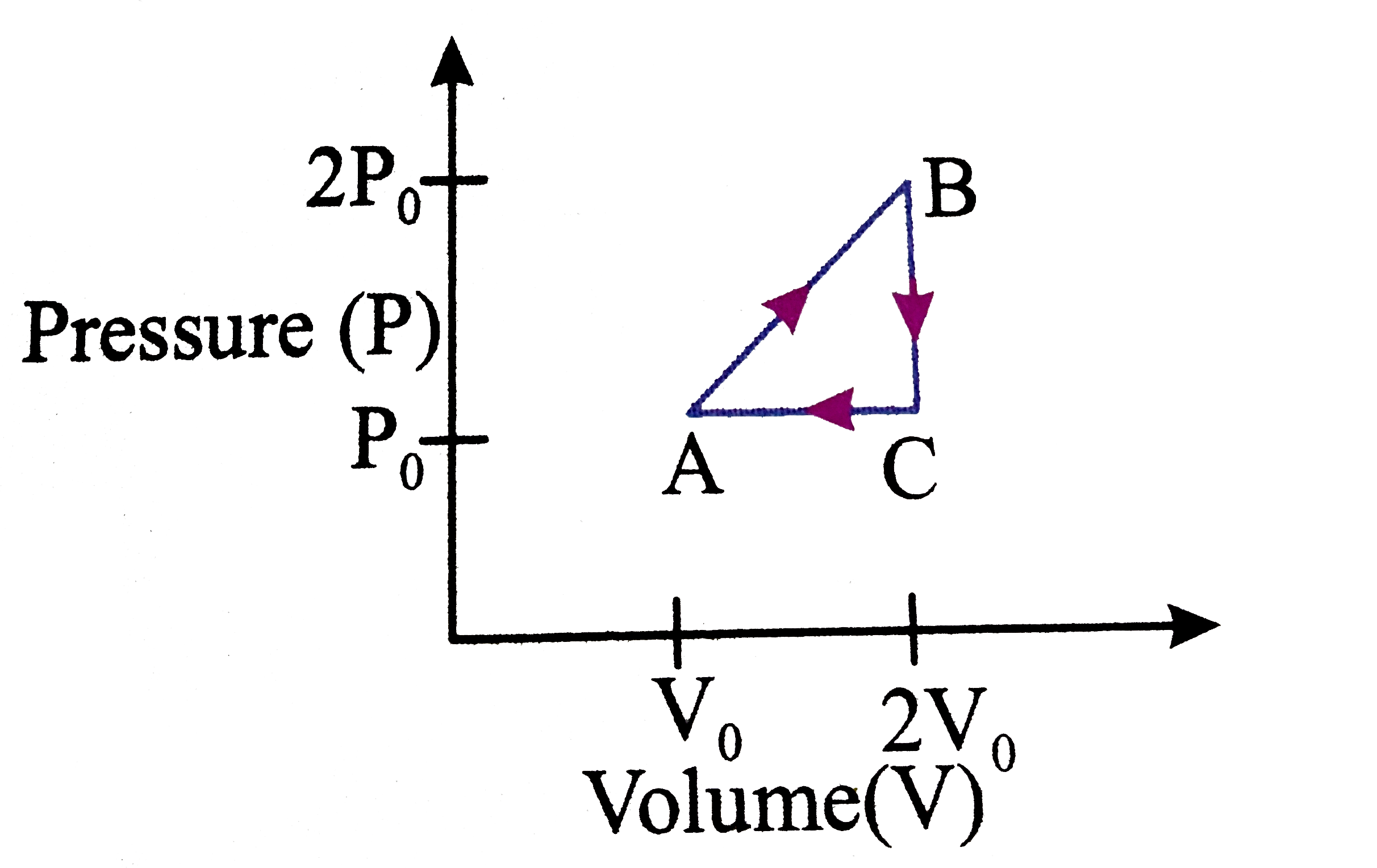
Let n be the number of moles of the gas and the temperature be T0 in the state A.
Now, work done during the cycle
W=12×(2V0−V0)(2P0−P0)=12P0V0
For the heat (ΔQ1) given during the process
A→B, we have
ΔQ1=ΔWAB+ΔUAB
ΔWAB= area under the straight line AB
=12(P0+2P0)(2V0−V0)=3P0V02
Applying equation of state for the gas in the state A & B.
P0V0T0=(2P0)(2V0)TB⇒TB=4T0
∴UAB=nCvΔT=n(5R2)(4T0−T0)
=15nRT22=15P0V02
∴ΔQ1=32P0V0+152P0V0=9P0V0
Obviously, the processes B→C and C→A
involve the abstraction of heat from the gas.
Efficiency=Work done per cycleTotal heat supplied per cycle
i.e., η=12P0V09P0V0=118
Related Playlists
- BOOK - NARAYNACHAPTER - KINETIC THEORY OF GASESEXERCISE - C.U.Q153videos
KINETIC THEORY OF GASES
- BOOK - NARAYNACHAPTER - KINETIC THEORY OF GASESEXERCISE - LEVEL-I(C.W)32videos
KINETIC THEORY OF GASES
- BOOK - NARAYNACHAPTER - KINETIC THEORY OF GASESEXERCISE - LEVEL-I (H.W)12videos
KINETIC THEORY OF GASES
- BOOK - NARAYNACHAPTER - GRAVITATIONEXERCISE - EXERCISE -IV40videos
GRAVITATION
- BOOK - NARAYNACHAPTER - LAW OF MOTIONEXERCISE - EXERCISE - IV35videos
LAW OF MOTION
Similar Questions
During the thermodynamic process shown in figure for an ideal gas
 View Solution
View SolutionFor the thermodynamic cycle shown in figure find (a) net output work of the gas during the cycle, (b) net heat flow into the gas per cycle.
 View Solution
View SolutionFor P-V diagram of a thermodynamic cycle as shown in figure, process BC and DA are isothermal. Which of the corresponding graphs is correct?
 View Solution
View Solution
An ideal undergoes a thermodynamic cycle as shown in figure. Which of the following graphs represent the same cycle?View SolutionOne mole of an ideal gas is carried through a thermodynamics cycle as shown in the figure. The cycle consists of an isochoric, an isothermal and an adiabatic process. Find the adiabatic exponent of the gas.
 View Solution
View SolutionIn the process shown in the figure on an ideal diatomic gas, the value of q and ΔH respectively is :
 View Solution
View SolutionIdeal gas is taken through process shown in figure :
 View Solution
View SolutionIdeal gas is taken through process shown in figure
 View Solution
View SolutionFigure shows the variations of the internal energy U With density ρ one mole an ideal monatomic gas for thermodynamic cycle ABCA . Here process AB is a part of rectangular hyperbola,-
_S01_092_Q01.png) View Solution
View SolutionPV Diagram for ideal gas in piston cylinder assembly undergoing a thermodynamic process is shown in figure. Process is
 View Solution
View Solution