Find the constants a and b in Moseley's equation √v=a(Z−b) from the following data.

Moseley's equation is
√v=a(Z−b)
Thus, √cλ1=a(Z1−b).....(i)
and √cλ2a=(Z2−b)....(ii)
From (i) and (ii) √c(1√λ1−1√λ1)=a(Z1−Z2 ,
or, a=√c(Z1−Z2)(1√λ1−1√λ2)
=(3×108m/s)1/242−27⎡⎢⎣1(71×10−12m)1/2−1(178.5×10−12m)1/2⎤⎥⎦
Dividing (i) by (ii)
√λ2λ1=Z1−bZ2−b
or , √178.571=42−b27−b
or, b=1.37
Related Playlists
- BOOK - RESONANCE ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Solved miscellaneous problems14videos
ATOMIC PHYSICS
- BOOK - RESONANCE ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Exercise 1 Part-1 subjective questions35videos
ATOMIC PHYSICS
- BOOK - RESONANCE ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - HIGH LEVEL PROBLEMS11videos
ALTERNATING CURRENT
- BOOK - RESONANCE ENGLISHCHAPTER - CAPACITANCEEXERCISE - High Level Problems16videos
CAPACITANCE
Similar Questions
Find the mean from the following data :
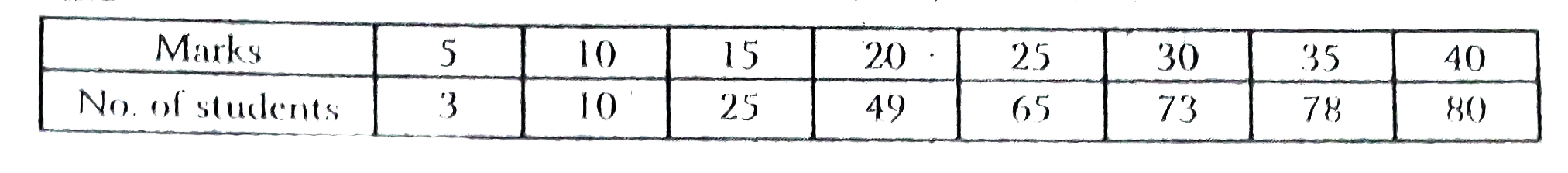 View Solution
View SolutionFind the median from the following data :
 View Solution
View SolutionFind the median from the following data :
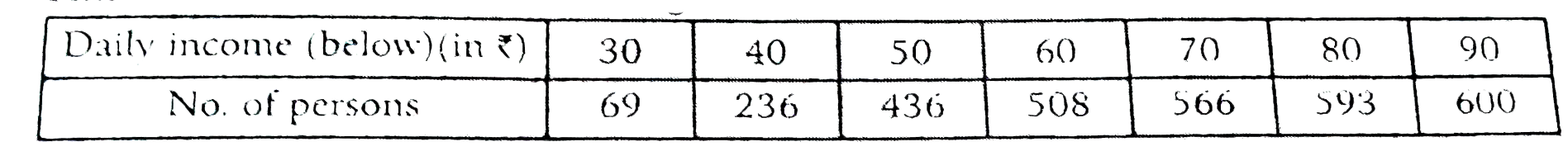 View Solution
View SolutionFind the median from the following data :
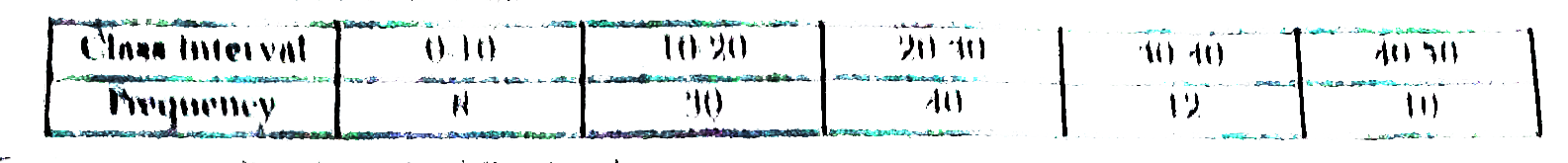 View Solution
View SolutionIn the graph between √vandZ for the Mosley's equation, √v=a(Z−b), the Mosley's equation, √v=a(Z−b), the intercept OX is 1 on √v axis.
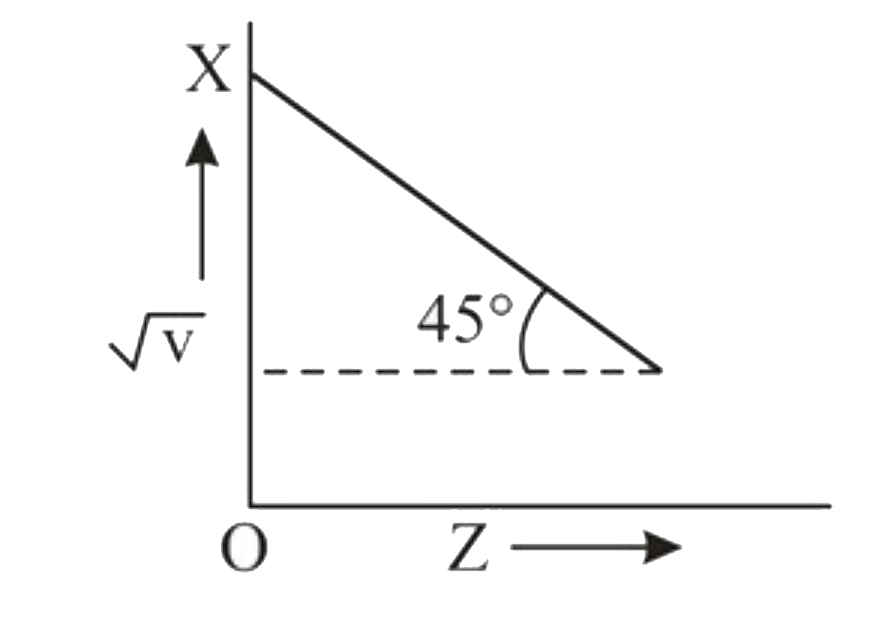
What is the frequency v when the atomic number Z is 52?View SolutionIn the graph between √v and Z for the Mosley's equation √v=a(Z-b), the intercept OX is -1 on √v axis.

What is the frequency when atomic number (Z) is 51?View SolutionFrom the following data, find
Regression equations.
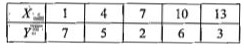 View Solution
View Solution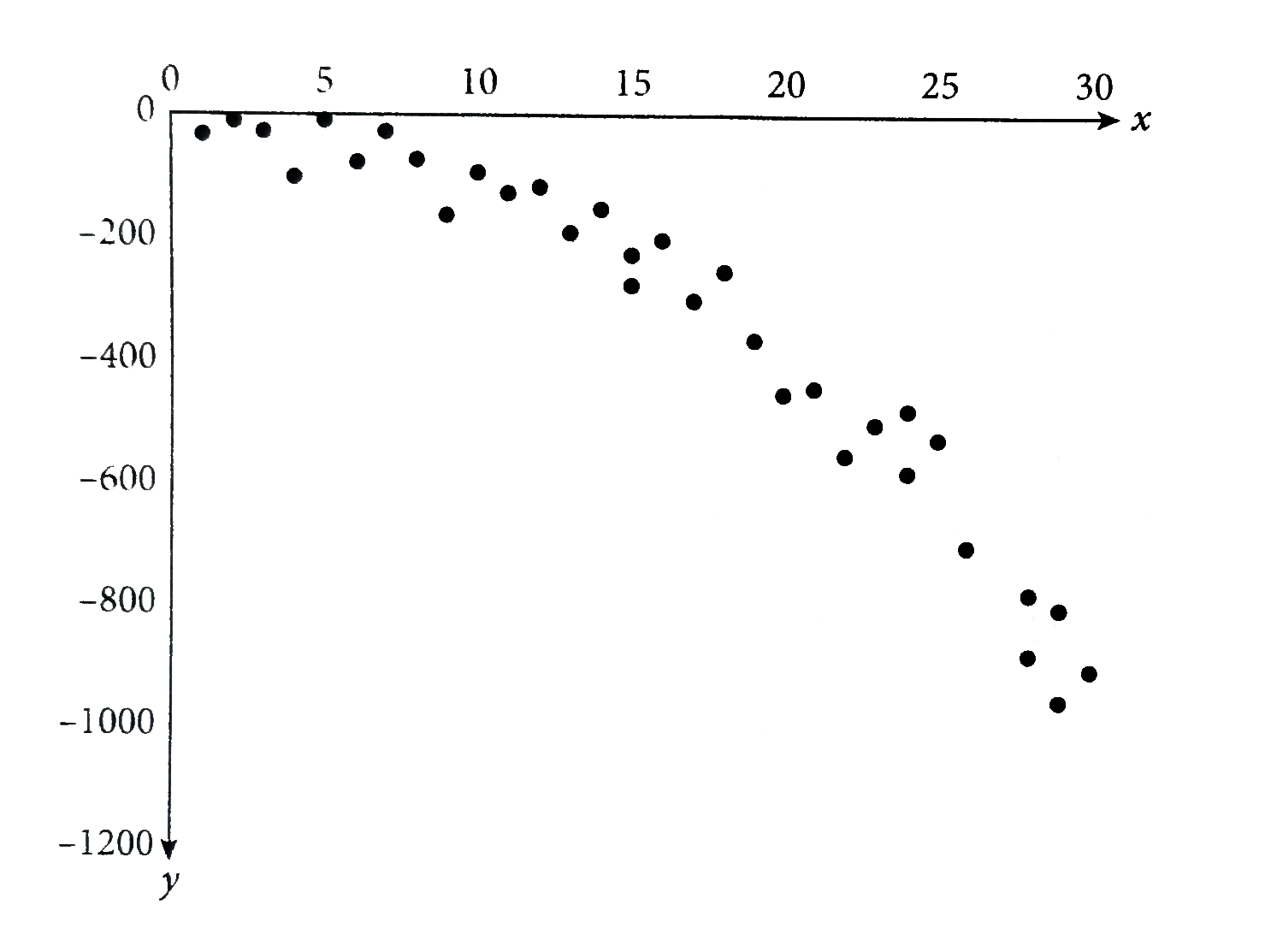
For which of the following values of a and b does the equation y=axb model the data in the scatterplot above ?View SolutionThe kα X-rays of aluminium (Z = 13 ) and zinc ( Z = 30) have wavelengths 887 pm and 146 pm respectively. Use Moseley\'s law √v=a(Z−b) to find the wavelength of the Kα X-ray of iron (Z = 26).
View SolutionThe kα X-rays of aluminium (Z = 13 ) and zinc ( Z = 30) have wavelengths 887 pm and 146 pm respectively. Use Moseley\'s law √v=a(Z−b) to find the wavelength of the Kα X-ray of iron (Z = 26).
View Solution


