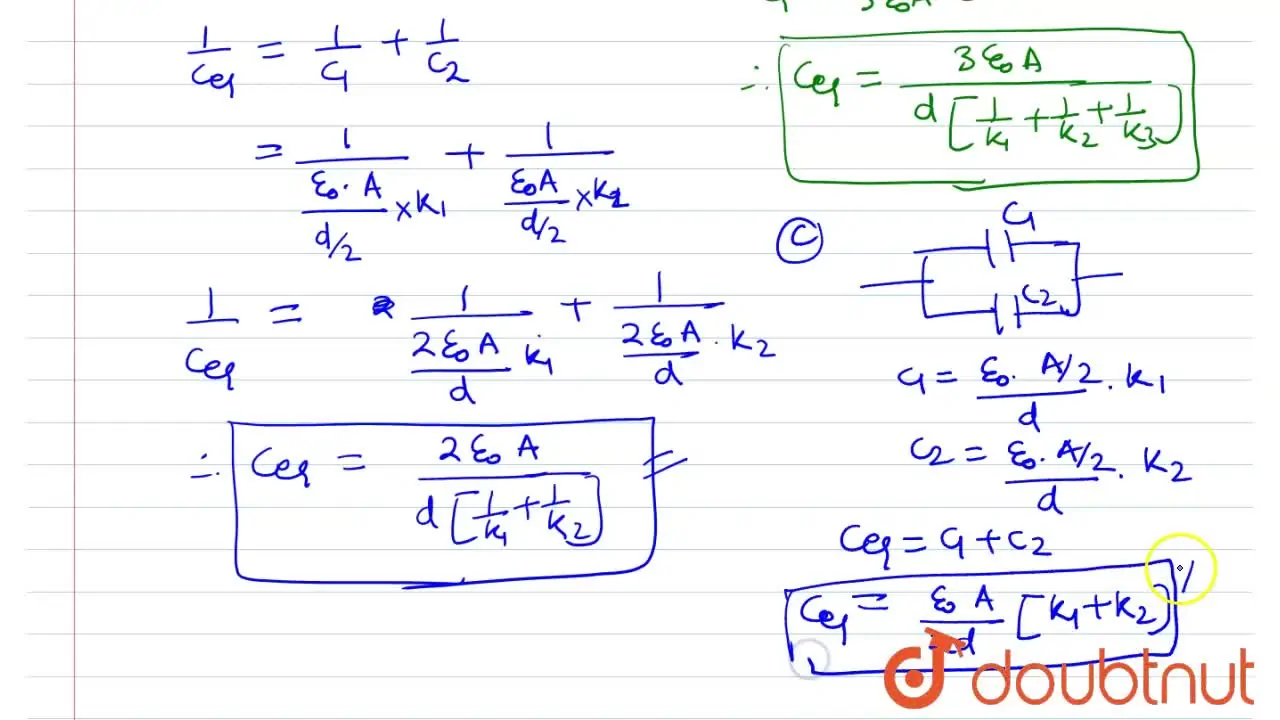
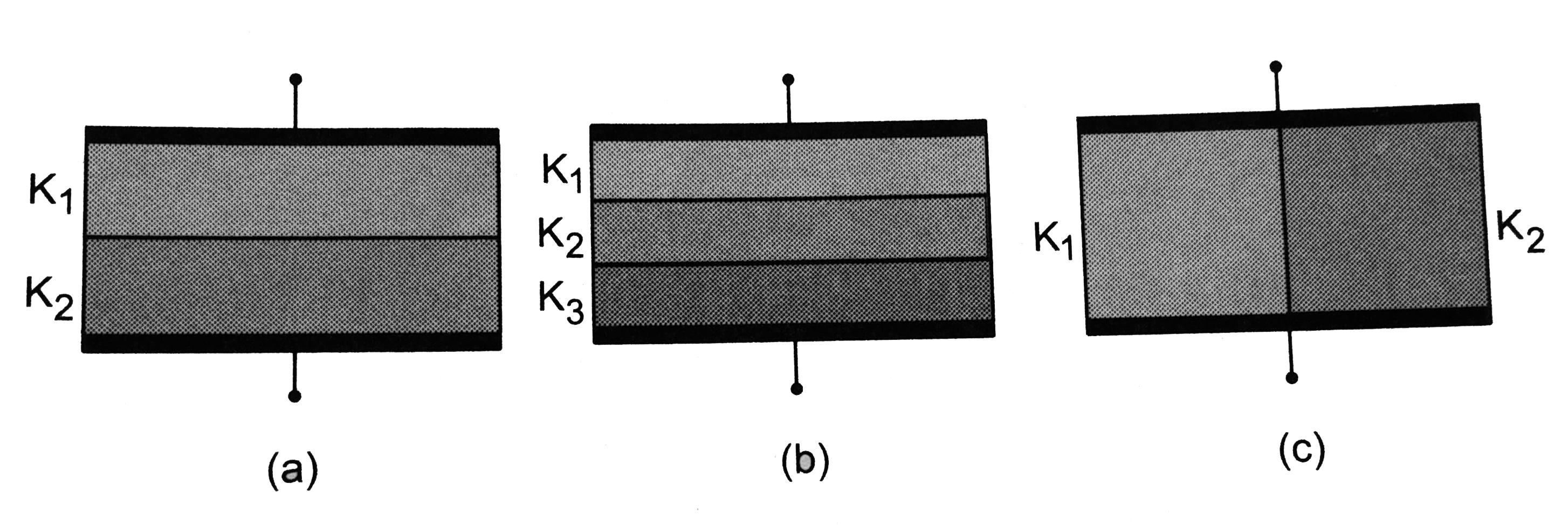
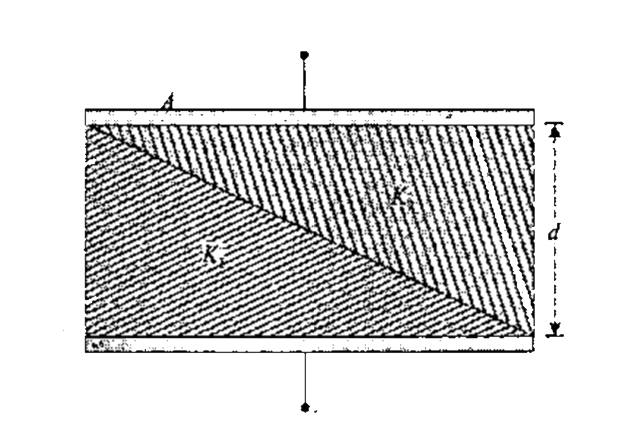
Find the capacitances of the capacitance of the capacitors shown In figure .The plate area is and the separation between the plate is . Different dielectric slabe in a particular part of the figure area of the same thickness and the entire gap between the plate is filled with the dielectric slabs.
(fig)
C_1 = K_1 epsilon_0 A / (d /3) = 3 K_1 epsilon_0 A / d C_2 = 3 K_2 epsilon_0 A / d
C = C_1 xx C_2 xx C_2 / C_1 C_2 + C_2 C_3 + C_3 C_1 = 3 epsilon_0 K_1 K_2 K_3 / K_1 K_2 + K_2 K_3 + K_3 K_1
C_2 = K_2 epsilon_0 A / 2d C = C_1 + C_2 = epslion_0 A / 2d (K_1 + K_2).
 ,
,

Related Playlists
- BOOK - HC VERMA ENGLISHCHAPTER - CAPACITORSEXERCISE - short answer7videos
CAPACITORS
- BOOK - HC VERMA ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE 26videos
CAPACITORS
- BOOK - HC VERMA ENGLISHCHAPTER - BOHR'S MODEL AND PHYSICS OF THE ATOMEXERCISE - Short Answer10videos
BOHR'S MODEL AND PHYSICS OF THE ATOM
- BOOK - HC VERMA ENGLISHCHAPTER - DISPERSION AND SPECTRAEXERCISE - Question for short Answer6videos
DISPERSION AND SPECTRA
Similar Questions
Find out the capacitance of parallel plate capacitor of plate area A and plate separation d.
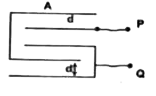
View SolutionThe equivalent capacitance between P and Q in the figure is (area of each plate is A and separation between two consecutive plates is d)
 View Solution
View SolutionFind the capacitance of a capacitor in which the space between the plates is partly filled with a dielectric (Fig. 25.5)
 View Solution
View SolutionFind the capacitance of a capacitor if the area of its plates is S, the distance between the plates is d0 and a dielectric sheet of the thickness d<d0 is inserted into the capacitor (Fig. 25.4)
 View Solution
View SolutionA parallel plate capacitor, with plate area A and plate separation d, is filled with a dielectric slabe as shown. What is the capacitance of the arrangement ?
View SolutionFind the equivalent capacitance between A and B.A: area of each plate, d: separation between the plates.
 View Solution
View SolutionThe capacitor shown has square plates of side L and has gap d between the photos. In the dielectric constant of the materiale of the slab is k , the capacitance of the capacitor is
 View Solution
View SolutionA parallel plate capacitor has plate area A and plate separation d. The space betwwen the plates is filled up to a thickness x (ltd) with a dielectric constant K. Calculate the capacitance of the system.
 View Solution
View SolutionIn a parallel-plate capacitor, the region between the plates is filled by a dielectric slab. The capacitor is connected to a cell and the slab is taken out. Then
View SolutionThe capacitance of a parallel plate capacitor with plate area A and separation d is C. The space between the plates in filled with two wedges of dielectric constants K1 and K2 respectively. Find the capacitance of resulting capacitor.
 View Solution
View Solution