Derive an expression for the magnetic induction at a nearby point of a straight and long current-carrying conductor. Discuss the nature of the magnetic lines of induction.
Consider a straight conductor XY carrying current I. Let us find its magnetic field at a point P at a perpendicular distance a from the point Q of the conductor, i.e. PQ = a
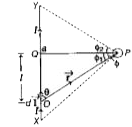
Let a small current element d1 of the conductor at point O. Let the distance of d1 from Q be l, i.e. OQ = l. Let r be the position vector of point P relative to the current element d1 and θ be the angle between d1 and r.
From Biot-Savart.s law, the magnitude of field dB due to current element d1 will be
dB=μ04π⋅Idlsinθr2
From right ΔOQP.
θ+ϕ=90∘⇒θ=90∘−ϕ
∴sinθ=sin(90∘−ϕ)=cosϕ
Also, cosϕ=ar
So, r=acosϕ=asecϕ
As, tanϕ=la
∴l=atanϕ
On differentiating, we get
dl=asec2ϕdϕ
Hence, dB=μ04πI(asec2ϕdϕ)cosϕa2sec2ϕ
dB=μ0I4πacosϕdϕ
The direction of magnetic field due to all such current elements will be normally into the plane of paper.
The total field B due to the entire conductor will be
B=∫ϕ2−ϕ1dB=μ0I4πa∫ϕ2−ϕ1cosϕdϕ
= μ0I4πa[sinϕ]ϕ2−ϕ1=μ0I4πa[sinϕ2−sin(−ϕ1)]
Hence, B=μ0I4πa[sinϕ1+sinϕ2]
Similar Questions
Magnetic induction at a point due to a small element of current carrying conductor is
View SolutionThe magnetic induction at any point due to a long straight wire carrying a current is
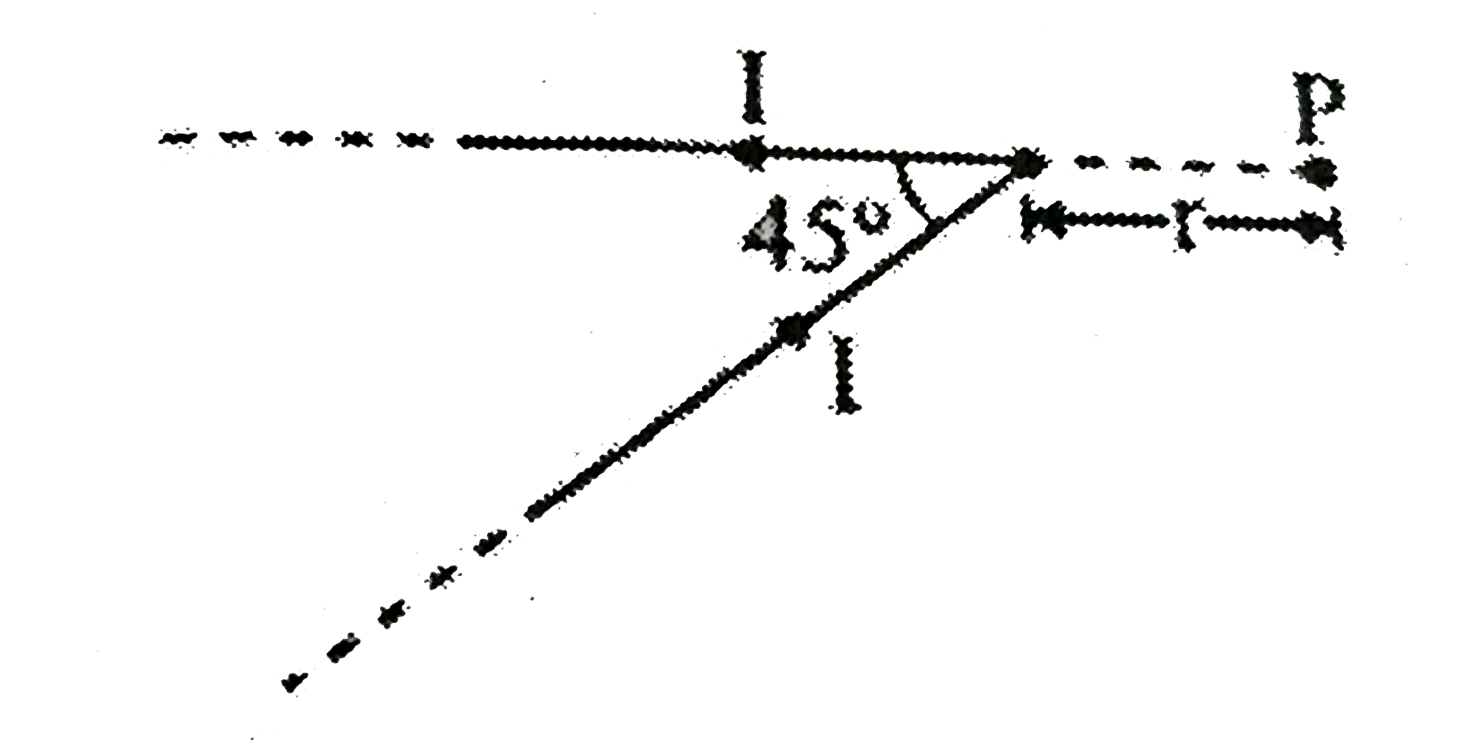
View SolutionMagnetic induction at point P from shown current-carrying long conductors is given by-
 View Solution
View SolutionMagnetic field at a point on the line of current carrying conductor is
View SolutionMagnetic lines of force around a current carrying conductor are circular.
View SolutionWrite the relation for the magnetic field induction at a point due to a linear conductor carrying current and hence deduce the relation for the magnetic field induction at a point due to a very long linear conductor carrying current.
View SolutionA long current carrying wire is bent as shown. The magnetic field induction at O is
 View Solution
View SolutionUsing Ampere's circuital law, obtain an expression for the magnetic induction at a point near an infinitely long straight conductor carrying an electric current.
View SolutionThe strength of the magnetic field around a long straight current carrying conductor :
View SolutionFind the magnetic induction due to a straight conductor of length 16cm carrying current of 5A at a distance of 6cm from the midpoint of conductor
View Solution

