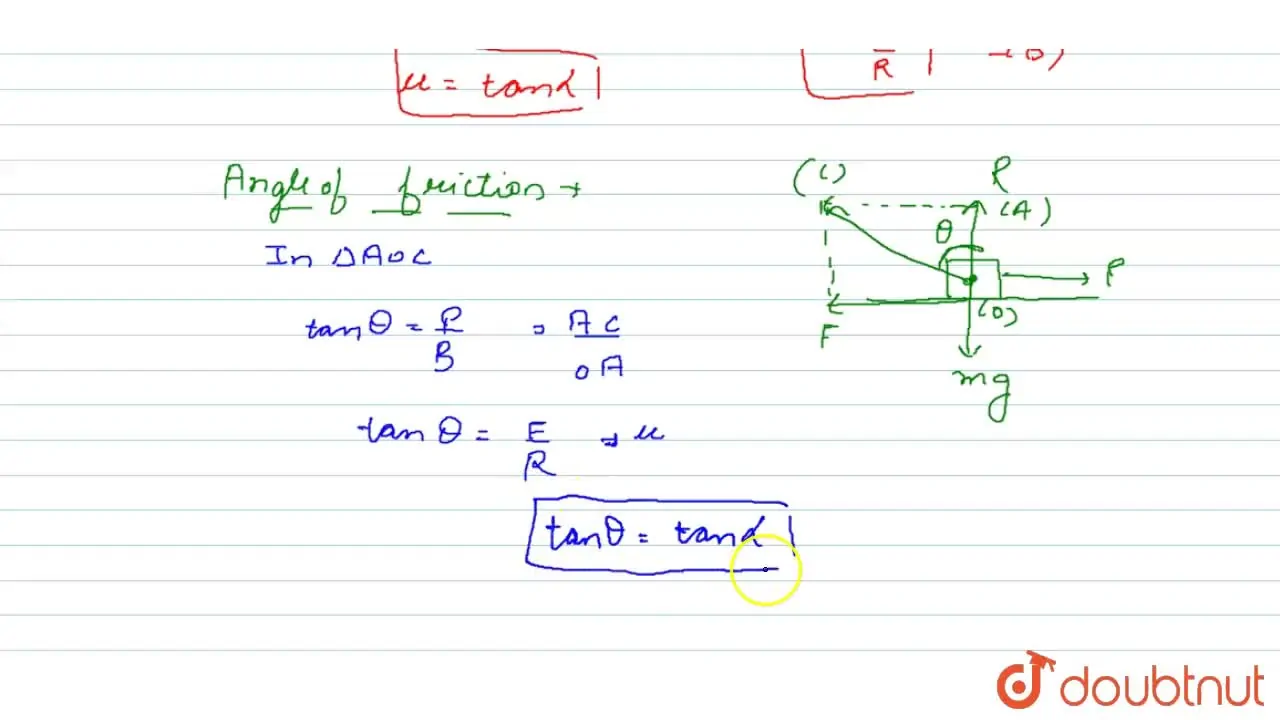
Define angle of repose and show that the coefficient of limiting friction is equalto tangent of repose. Hence show that angle of epose is equal to angle of friction.Solution in Punjabi
Angle of friction: Angle between normal reaction and resultant of limiting friction and normal is known as angle of friction
The resultant of limiting friction (F) and normal reaction (R) is represented by R. in the figure. Angle θ between R and R. is called angle of friction.
From figure,
tanθ=FR
But FR=μs∴tanθ=μs .......(i)
Angle of repose: It is the minimum angle made by the inclined plane with the horizontal plane such that the body placed on inclined plane just begins to slide.
Let α be the angle made by inclined plane with horizontal plane. From figure(ii), we have
R=mgcosα and F=mgsinα
∴FR=mgsinαmgcosα=tanα
But FR=μs=tanα .....(ii)
From equation (i) and (ii) we get tanθ=tanα⇒θ=α .........(iii)
Thus angle of friction is equal to angle of repose

Similar Questions
Consider the following statements
A) Angle of repose is equal to angle of friction
B) Angle of friction is independent of coefficient of friction03:19View SolutionConsider the following statements
(A) Angle of repose is equal to angle of friction
(B) Angle of friction is independent of coefficient of frictionView SolutionDefine angle of friction and angle of repose. Show that both are numerically equal.
04:10View SolutionConsider the following statements (A) Angle of repose is equal to angle of friction (B) Angle of friction is independent of coefficient of friction
View SolutionDefine angle of friction and angle of repose and show that they are equal to each other:
06:15View SolutionDefine angle of repose. Is this angle equal to the angle of friction ?
03:54View SolutionStatic and Kinetic Friction|| Angle OF Friction|| Angle OF Repose
33:44View SolutionAngle OF Friction and Angle OF Repose
38:38View Solution