Deduce the relation for the magnetic induction at a point due to an infinitely long straight conductor carrying current. Solution in Tamil
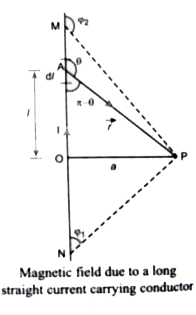
Magnetic field due to long straight conductor carrying current:Conside a long straight in wire NM with current I flowing from N to M.Let P be the point at a distance a from point O.Consider an element of length dl of the wire at a distance l from point O and ¯r be the vector joining the element dl with the point P.Let θ be the angle between ¯¯¯dl and ¯r,Then ,the magneti field at P due to the elements is
d¯¯¯B=μ0Id¯l4πr2sinθ( unit vector perpendicular to d¯land¯r)
The direction of the fie1ld is perpendicular to the1 plane of the paper and going into it.This can be determined by taking the1 cross product betw1e1e1n to ve1cors d¯and ¯r (Let it be ∩n).The net magnetic field can be determined by intergrating with proper limits.
¯¯¯B=∫d¯¯¯B
From the figure,ina right angle triangle PAO,tan(π−θ)=al
l=−atanθ(sintan(π−θ)=−tanθ)⇒1tanθ=cotθ
l=−acotθandr=acosecθ
Differentiating,
dl=acosec2θdθ
d¯¯¯B=μ9I(acosec2θdθ)4π(acosecθ)2sinθdθˆn=μ0I(acosec2θdθ)4πa2cosec2θsinθdθˆn
d¯¯¯B=μ0I4πasinθdθˆn
This is the magetic field at a point P due to the current in small elemental length.Note that we have expressed the magnetic field OP in terms of angular coordinate i.e θ .Therefore,the net magnetic field at the point P which can be obtained by intergrating d¯¯¯B by varying the angle from θ=Φ1→θ−Φ2 is
¯¯¯B=μ0I4πra∫Φ2Φ1sinθdθˆn=μ0I4πa(cosΦ1−cosΦ2)ˆn
For a an infinitely long straight wire ,1=0 and 2=,the magnetic field is ¯¯¯B=μ0I2πaˆn....(3)Note that here ˆn represents the unit vector from the point O to P.
Related Playlists
- BOOK - FULL MARKSCHAPTER - SAMPLE PAPER-8EXERCISE - PART-III9videos
SAMPLE PAPER-8
- BOOK - FULL MARKSCHAPTER - SAMPLE PAPER-6EXERCISE - PART - III18videos
SAMPLE PAPER-6
- BOOK - FULL MARKSCHAPTER - SEMICONDUCTOR ELECTRONICSEXERCISE - Additional Question(Numerical problems.)6videos
SEMICONDUCTOR ELECTRONICS
Similar Questions
A water molecule has an electric dipole moment of 6.3×10−30 cm . A sample contains 1022 water molecules with all the dipole moments aligned parallel to the external electric field of magnitude 3×105NC−1 . How much work is required to rotate all the water molecules from θ=0∘to90∘ ?
02:57View SolutionDefine capacitance . Give its unit.
03:06View SolutionIf the energy of a photon of sodium light (λ=589nm) equals the band gap of a semiconductor, calculate the minimum energy required to create hole-electron pair.
01:24View SolutionWrite the relation for the magnetic field induction at a point due to a linear conductor carrying current and hence deduce the relation for the magnetic field induction at a point due to a very long linear conductor carrying current.
02:54View SolutionThe magnetic induction due to an infinitely long straight wire carrying a current i at a distance r from wire is given by
03:48View SolutionThe magnetic induction at any point due to a long straight wire carrying a current is
11:14View SolutionUsing Ampere's circuital law, obtain an expression for the magnetic induction at a point near an infinitely long straight conductor carrying an electric current.
11:14View SolutionFind the magnetic induction due to a long current carrying conductor.
11:14View SolutionDeduce the relation for the magnetic induction at a point due to an infinitely long straight conductor carrying current.
04:30View SolutionDeduce the relation for the magnetic induction at a point due to an infinitely long straight conductor carrying current.
05:41View SolutionDeduce the relation for the magnetic induction at a point due to an infinitely long straight conductor carrying current.
01:23View SolutionMagnetic induction at a point due to a small element of current carrying conductor is
View SolutionDerive an expression for the magnetic induction at a nearby point of a straight and long current-carrying conductor. Discuss the nature of the magnetic lines of induction.
View SolutionThe shape of the magnetic lines of force due to an infinite, long, straight current carrying conductor is
View SolutionWrite an expression for magnetic induction due to a long straight conductor carrying current I.
View Solution


