_E01_109_Q01.png)
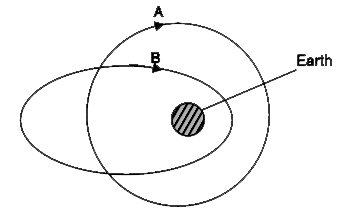
Consider two satellites A and B of equal mass m, moving in the same circular orbit of radius r around the earth E but in opposite sense of rotation and therefore on a collision course (see figure)
(i). In terms of G,Me m and r find the total mechanical energy EA+EB of the two satellite plus earth system before collision
(ii). If the collision is completely inelastic so that wreckage remains as one piece of tangled material (mass=2m) find the total mechanical energy immediately after collision.
(iii). Describe the subsequent motion of the wreckage.Solution in Gujrati
The correct Answer is:(i). −GmMer
(ii). −2GmMer
(iii). Free fall
By applying conservation of linear momentum
m(v)−m(v)=2mv',v'=0
Initially energy of a satellite 'A' and 'B' is
EA=−GMem2R,EB=−GMem2R
Total enegy EA+EB=−GMemR
After collision velocity of satellite becomes zero then the K.E.=0 therefore total mechanical energy becomes
−GMe2MR
Related Playlists
- BOOK - ALLEN CHAPTER - GRAVITATIONEXERCISE - Exercise 5 A (Previous Year Questions)26videos
GRAVITATION
- BOOK - ALLEN CHAPTER - GRAVITATIONEXERCISE - Exercise 5 B (Previous Year Questions)9videos
GRAVITATION
- BOOK - ALLEN CHAPTER - GRAVITATIONEXERCISE - Exercise 4 A (Conceptual Subjective Exercise)14videos
GRAVITATION
- BOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective14videos
GEOMETRICAL OPTICS
- BOOK - ALLEN CHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)47videos
KINEMATICS-2D
Similar Questions
If suddenly the gravitational force of attraction between earth and satellite revolving around it becomes zero, then the satellite will
04:07View SolutionA satellite S is moving in an elliptical orbit around the earth. The mass of the satellite is very small compared to the mass of the earth.
03:03View Solution_E01_076_Q01.png)
In the given figure L=1 metre if total gravitational force on 4 kg mass is →F1 and on 2 kg mass is →F2 then find out the ratio of ∣∣∣→F1→F2∣∣∣View SolutionA prism of refractive index n1 & another prism of reactive index n2 are stuck together without a gap as shown in the figure.The angle of the prisms are as shown. n1&n2depend onλ,the wavelength of light according to n1=1.20+10.8×104λ2&n2=1.45+1.80×104λ2 where λ is in nm.

(i)Calculate the wavelength λ0for which rays incident at any angle on the interfaceBCpass through without bending at that interface.
(ii) for light of wavelength λ0,find the angle of incidencei on faceACsuch that the deviation produced by the combination of prism is minimum.View SolutionA particle is moving in xy-plane .At certain instant the components of its velocity and acceleration are as follows ux=3m/s,uy=4m/s,ax=2m/s2anday=1m/s2. The rate of change of speed at this moment is
07:50View SolutionConsider two satellites A and B of equal mass, moving in the same circular orbit of radius r around the earth but in the opposite sense and therefore a collision occurs. (a) Find the total mechanical energy E_(A) + E_(B) of the two satellite-plus-earth system before collision. (b) If the collision is completely inelastic, find the total mechanical energy immediately after collision. Describe the subsequent motion of the combined satellite.
03:49View SolutionConsider two satellites A and B of equal mass m , moving in the same circular orbit about the earth, but in the opposite sense as shown in Fig. The orbital radius is r . The satellites undergo a collision which is perfectly inelastic. For this situation, mark out the correct statement(s). [Take mass of earth as M ]
02:13View SolutionSatellite A is following a circular path of radius a around the earth another satellite B follows an elliptical path around the earth. The two satellites have same mechanical energy and their orbits intersect. Find the speed of satellite B at the point where its path intersects with the circular orbit of A. Take mass of earth to be M.
 05:09View Solution
05:09View SolutionTwo satellite of same mass are launched in the same orbit of radius r around the earth so as to rotate opposite to each other. If they collide inelastically and stick together as wreckage, the total energy of the system just after collision is
03:50View SolutionMatch the Column I with Column II
For a satellite in circular orbit
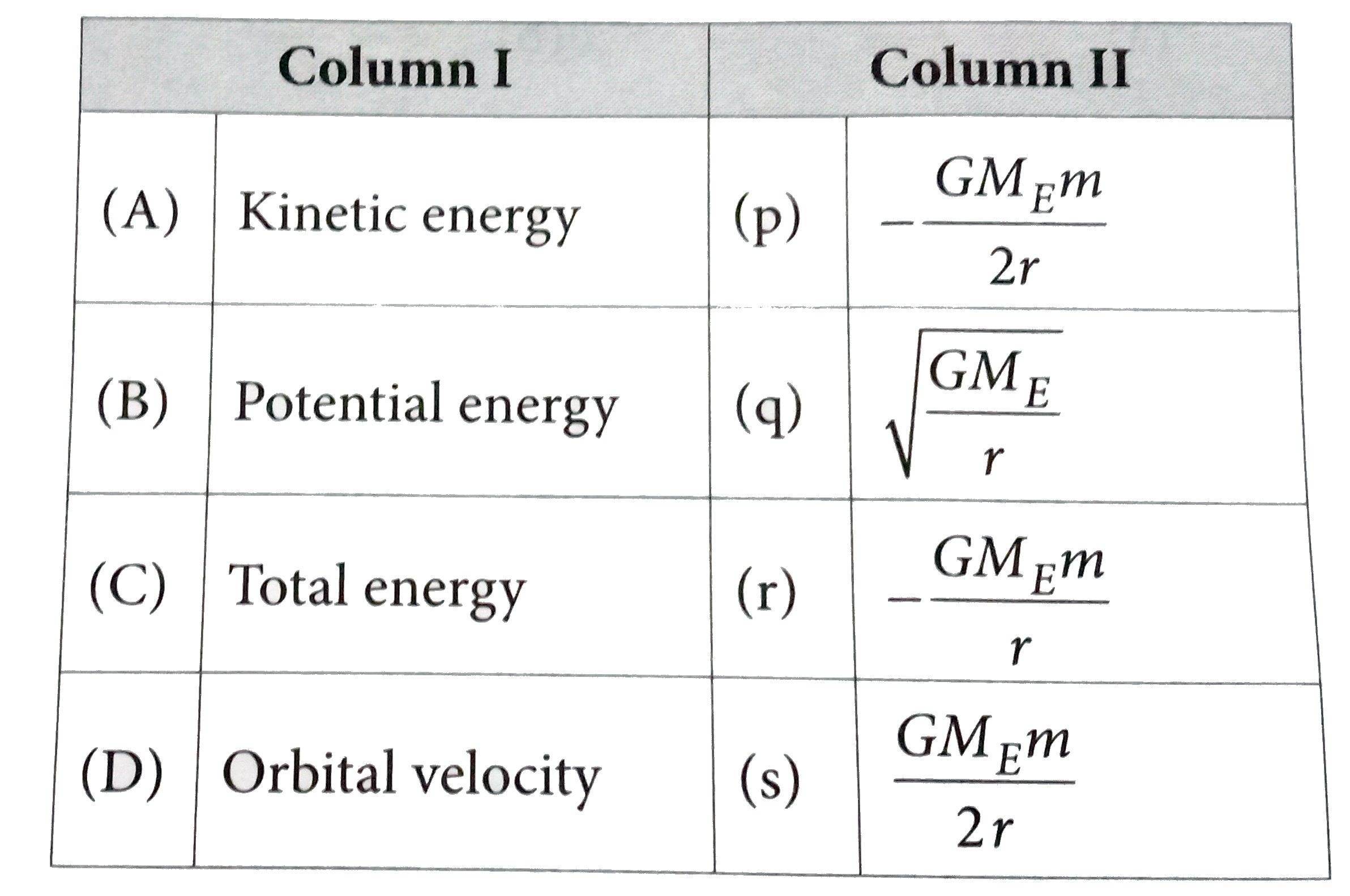
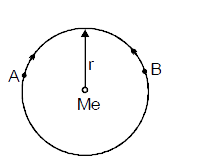
(where ME is the mass of the earth , m is the mass of the satellite and r is the radius of the orbit )02:02View SolutionConsider two satellites A and B of equal mass m, moving in the same circular orbit of radius r around the earth E but in opposite sense of rotation and therefore on a collision course (see figure).
In terms of G, Me, m and r find the total mechanical energy EA + EB of the two satellite plus earth system before collision.
 View Solution
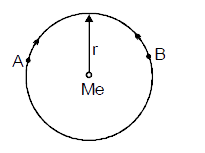
View SolutionConsider two satellites A and B of equal mass m, moving in the same circular orbit of radius r around the earth E but in opposite sense of rotation and therefore on a collision course (see figure).
If the collision is completely inelastic so that wreckage remains as one piece of tangle d material (mass = 2m), find the total mechanical energy immediately after collision.
 02:56View Solution
02:56View Solutionएक उपग्रह पृथ्वी के चारों ओर त्रिज्या r की कक्षा में चाल v से घूम रहा है | यदि उपग्रह का द्रव्यमान M है तो उसकी कुल ऊर्जा होगी :
View Solutionm, द्रव्यमान का एक उपग्रह पृथ्वी के चारों ओर r त्रिज्या के वृत्तीय मार्ग में परिक्रमा कर रहा है । यदि पृथ्वी का द्रव्यमान Me हो तो सिद्ध कीजिए कि उपग्रह का कोणीय संवेग √Gm2Mer होगा ।
05:29View Solutionm द्रव्यमान का एक उपग्रह,M द्रव्यमान के ग्रह के चारों ओर R त्रिज्या की वृत्तीय कक्षा में घूम रहा है, तो इसकी कुल ऊर्जा E होगी :
01:04View SolutionA satellite of mass m is moving in a circular orbit of radius r = (R_(e) + h) around earth of radius R_(e) and mass M_(e) , and density of earth rho . Match the following
04:54View Solution


