Consider the moment of inertia I of the rigid homogeneous disc of mass M as shown in the figure about an axis passing through its centre (different shadings only differentiate the two parts of the disc each with equal mass M/2). Which one of the following statements concerning I is correct? 
The inner and outer parts of the disc, each with mass M/2, contribute equal amounts to /.
The inner part of the disc contributes less to// than outer part.
The inner part of the disc contributes less to//than the outer part.
The inner part of the disc may contribute more or less to//depending on the actul numerical value to the mass M of the disc.
The correct Answer is:C
Step by step video & image solution for Consider the moment of inertia I of the rigid homogeneous disc of mass M as shown in the figure about an axis passing through its centre (different shadings only differentiate the two parts of the disc each with equal mass M//2). Which one of the following statements concerning I is correct? by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Related Playlists
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - A Only One Option is Correct86videos
ROTATIONAL MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - More than one option is correct36videos
ROTATIONAL MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions2videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct3videos
SEMICONDUCTORS AND ELECTRONIC DEVICES
Similar Questions
Calculate the moment of inertia of a rod of mass M, and length l about an axis perpendicular to it passing through one of its ends.
View SolutionThe moment of inertia of a hollow cubical box of mass M and side a about an axis passing through the centres of two opposite faces is equal to.
View SolutionMoment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
View SolutionFind the moment of inertia of a uniform rectangular plate of mass M and edges of length 'I' and 'b' about its axis passing through the centre and perpendicular to it.
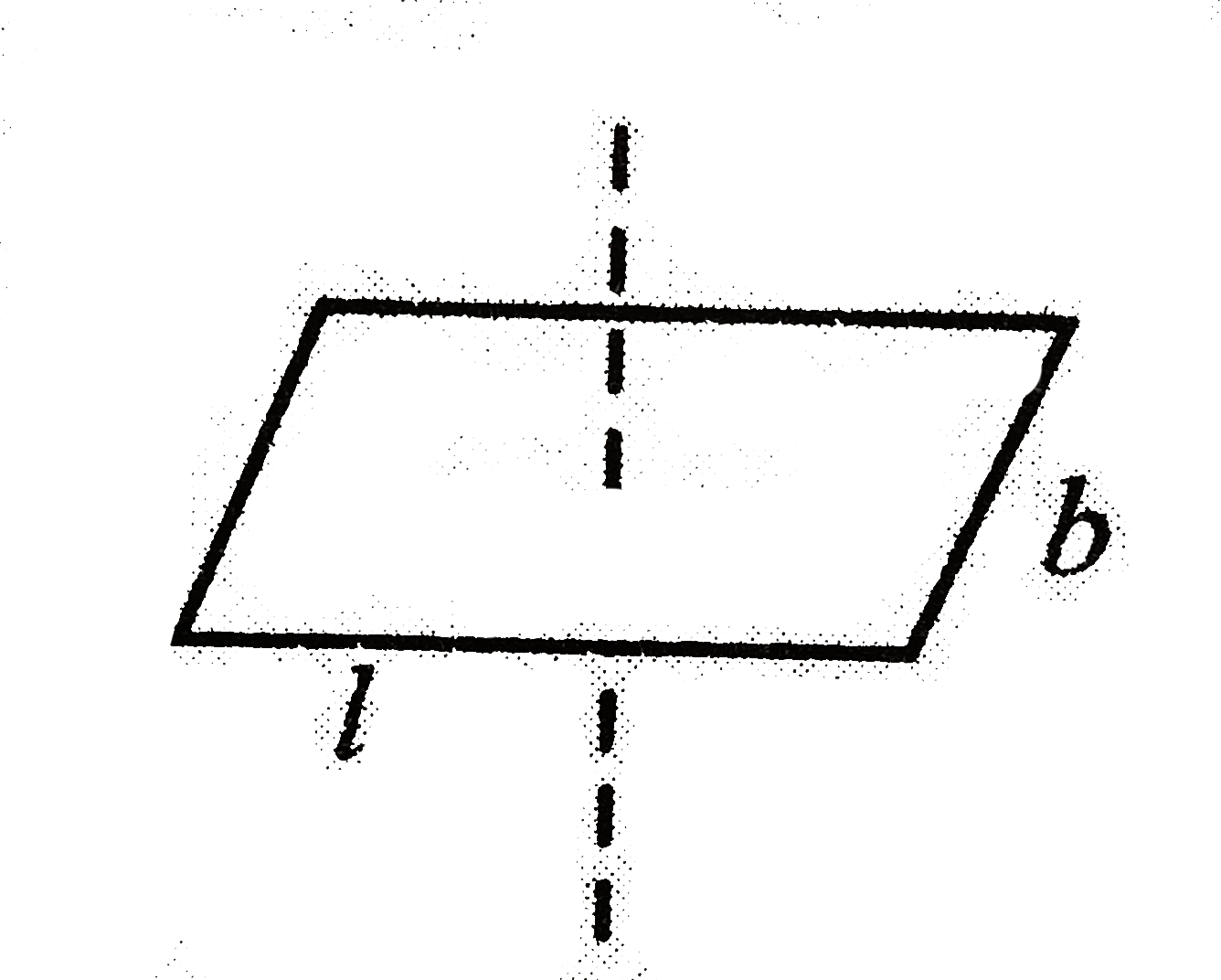 View Solution
View SolutionCalculate the moment of inertia of a.unifprm disc of mass 0.4 kg and radius 0.1m about an axis passing through its edge and perpendicular to the plane of die disc ?
View SolutionThe moment of inertia of a cube of mass M and edge length a about an axis passing through one of its edge is
View SolutionThe moment of inertia of a uniform rod of length 2l and mass m about an axis xy passing through its centre and inclined at an enable α is
 View Solution
View SolutionThe moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
View SolutionMoment of inertia of a uniform quarter disc of radius R and mass M about an axis through its centre of mass and perpendicular to its plane is :
View SolutionMoment of inertia of a uniform quarter disc of radius R and mass M about an axis through its centre of mass and perpendicular to its plane is :
View Solution


