By stating sign conventions and assumptions made,derive mirror formula for a concave mirror.Solution in Punjabi
For sign conventions, see Long Answer Type Question.No. 1
Let AS be an object placed on the-principal axis of a convex mirror as shown in Fig. The ray of light from point i?of the object travelling parallel to the principal axis falls at point Eon the mirror and is reflected along EQ, such that it appears to come from focus (F) of the convex mirror. Another ray of light incident at pole is reflected according to the laws of reflection along PQ.i.e.∠BPA=∠QPA . Also, the ray of light from point B incident on the mirror towards point C along BK will be reflected back and it will also appear to come from point B. The rays EQ, PQ and KB
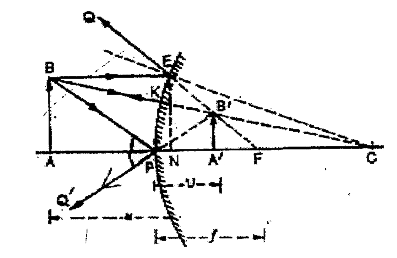
appear to come from point B. , so that the point B is image of the point B of the object. In the same manner, the image of every point on object AB will be produced at a corresponding point on AB, so that A.B is the virtual image of the object AB as formed by the convex mirror. From point E, drop EN perpendicular to the principal axis.
Now, triangles A.BF and ENFate similar. Therefore,
ABNE=AFNF
As aperture of the convex mirror is small, also, NF = PF and NE = AB
Therefore, ABAB=AFPF
Since, the distances are to be measured from pole of the mirror, we have . A.F= PF-PA.
∴ABAB=PF−PAPF.....(i)
Also, triangles ABP and A.BPare similar. Therefore,
A.B.AB=PA.PA.........(ii)
From equations (i) and (ii), we have
PF−PAPF=PAPA..........(iii)
Applying sign conventions, we have:
PA=+u
PA.=+v
PF=+f
Substituting for PA, PA. and PF.m equation (iii), we have
+f−(+v)+f=+v−u or f−vf=−vu
or 1−vf=−uv
Divide throughout by v.
1v−1f=−1u
or 1u+1v=1f
which is the required mirror formula.
Related Playlists
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - REFLECTION OF LIGHT EXERCISE - MOST EXPECTED QUESTIONS (1 Mark)3videos
REFLECTION OF LIGHT
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - REFLECTION OF LIGHT EXERCISE - MOST EXPECTED QUESTIONS (2 Marks)4videos
REFLECTION OF LIGHT
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - REFLECTION OF LIGHT EXERCISE - SHORT ANSWER TYPE QUESTIONS (3 Marks)1videos
REFLECTION OF LIGHT
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - RADIOACTIVITY EXERCISE - MOST EXPECTED QUESTIONS6videos
RADIOACTIVITY
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - REFRACTION OF LIGHTEXERCISE - NUMERICAL PROBLEMS36videos
REFRACTION OF LIGHT
Similar Questions
What is the minimum size of the plane mirror , in which a man can see his full height?Explain.
09:25View SolutionDifferentiate between a real image and a virtual image.
03:40View SolutionWhen an object is placed beyond centre of curvature of a concave mirror, the image is formed:
00:52View SolutionWhat are γ-rays?
05:35View SolutionA convex lens of refractive index 1.5 has a focal length of 18 cm in air.Calculate the change in focal length,when it is immersed in water of refractive index 4/3.
21:20View SolutionMirror Formula And Sign Convention
01:47View SolutionState and explain sign conventions used in spherical mirrors.
04:57View Solutionनिर्देशांक चिन्ह परिपाटी के अनुसार अवतल दर्पण की फोकस दूरी ................... होती है ।
58:53View Solutionनिर्देशांक चिह्न परिपाटी के अनुसार दर्पण-सूत्र है
View SolutionIntroduction to Spherical Mirror |Important terms|sign convention|Mirror formula|magnification
02:25View SolutionWhat are cartesian sign conventions used in spherical mirror ? What is the mirror formula ?
07:58View Solution(a) With the help of a suitable ray diagram, derive the mirror formula for a concave mirror.
10:24View SolutionSpherical Mirror||Sign Convention||Mirror Formula||Magnification
05:12View Solution9. According to the "New Cartesian Sign. Convention" for mirrors, what sign has been given to the focal length of i) a concave mirror ii) a convex mirror
00:42View Solutionनिर्देशांक चिह्न परिपाटी के अनुसार अवतल दर्पण की फोकस-दूरी _______ होती हैI
10:24View SolutionDerive mirror formula for concave mirror stating assumptions?
02:43View Solution


