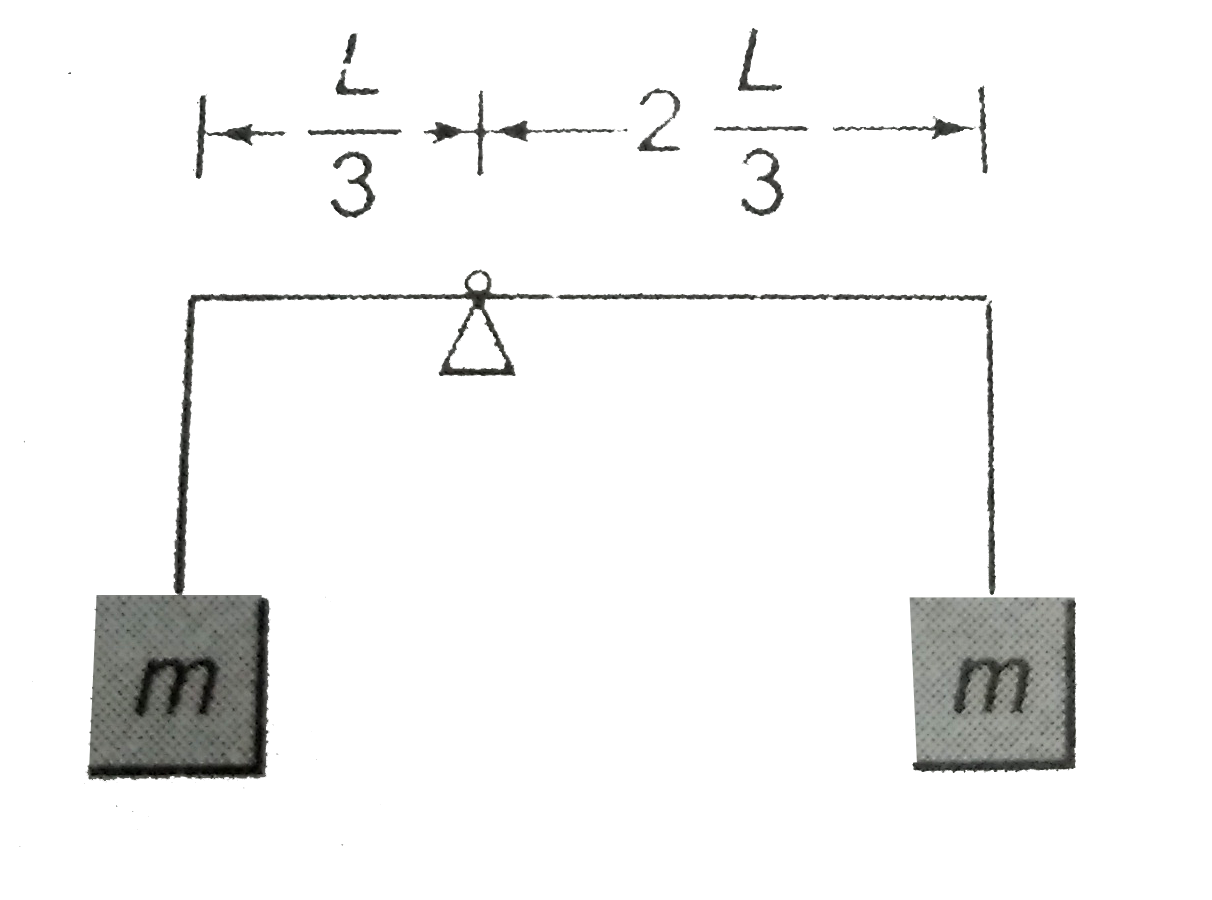
As shown in the figure, two blocks, each of mass m, suspended from the ends of a rigid light rod of length L. The rod is held horizontally on the fulcrum and then released.
(a) Find the initial angular acceleration of the rod.
(b) If the mass of rod is also m uniformly distributed. find the tension in the strings attached to blocks.
(a) 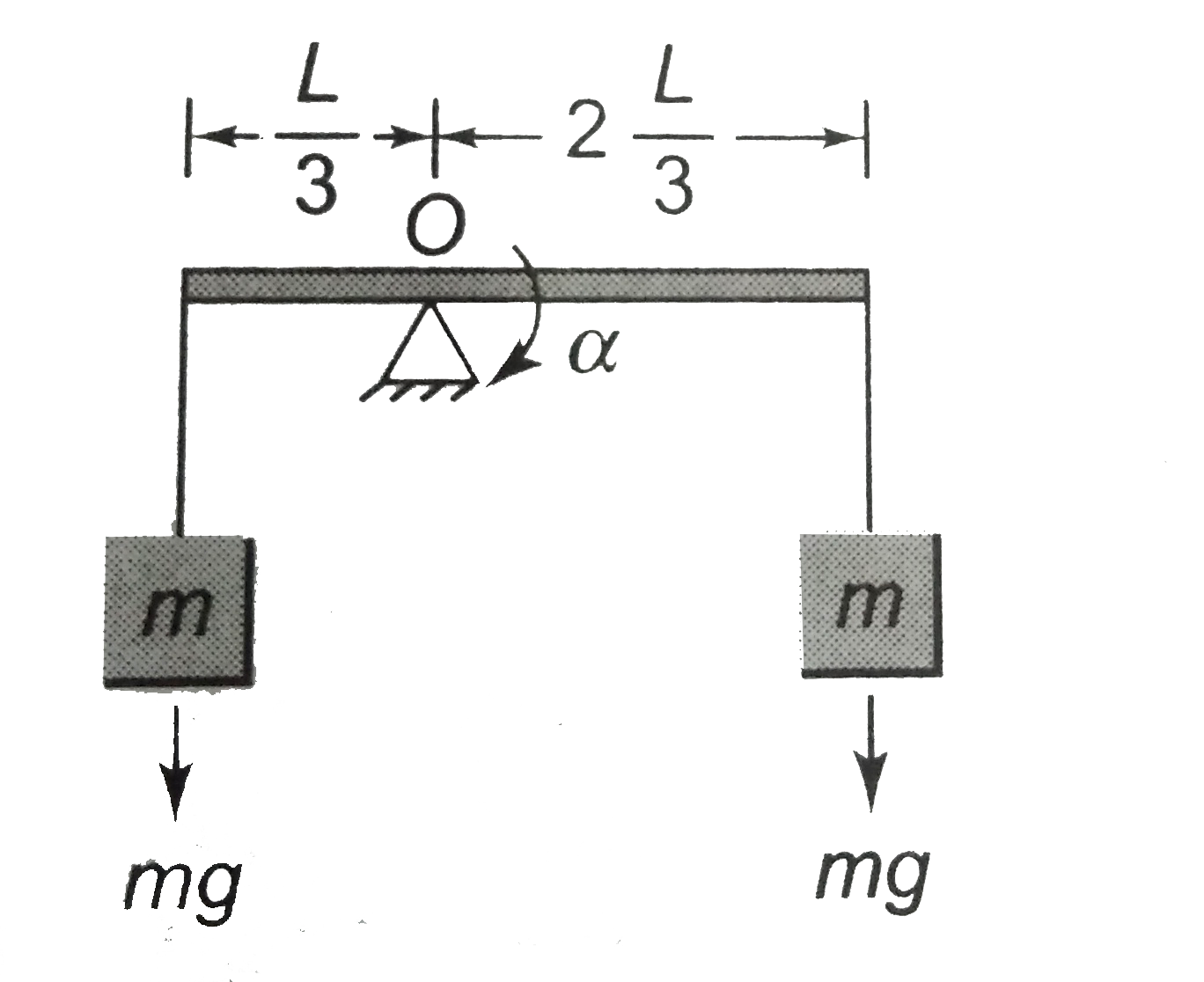
Consider (block s + rod) as system.
Taking torque about O
τ0=mg×2L3−mg×L3=I0α
=[m(2L3)2+m(L3)2]α
mgL3=59mL2α⇒α=3g5L
(b) 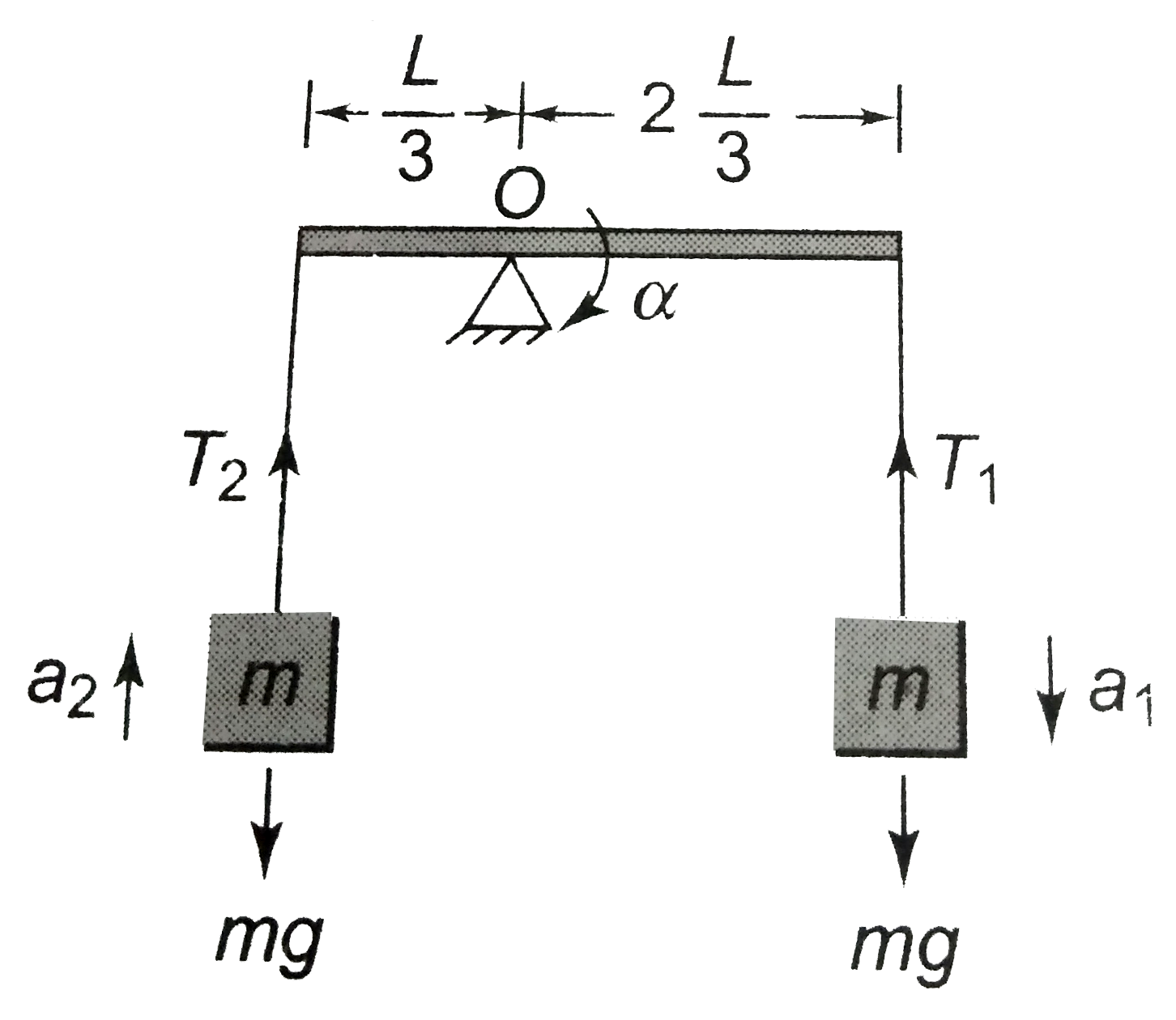
Now the rod has mass m. Its moment of inertia about O
I'=mL212+m(L2−L3)2=mL212+mL236=mL29
Considering (block + rod) as a system and taking torque about O
τ0=mg×2L3−mg×L3=I0α
=[m(2L3)2+m(L3)2+mL29]α
mgL3=23mL2α⇒α=82L
a1=2L3α=2L3×82L=83
mg−T1=ma1⇒T1=m(g−a1)=2mg3
a2=L3α=L3×gL=86
T2−mg=ma2⇒T2=m(g+a2)=7mg6
Topper's Solved these Questions
Similar Questions
Figure shows particles 1 and 2, each of mass m, fixed to the ends of a rigid massless rod of length L1+L2,with L1=20cmandL2=80cm. The rod is held horizontally on the fulcrum and then released. What are the magnitudes of the initial accelerations of (a) particle 1 and (b) particle 2?

View SolutionA rod PQ of mass M and length L is hinged at end P. The rod is kept horizontal by a masseless string tied to point Q as shown in Fig. When string is cut, the initial angular acceleration of the rod is :

View Solution
Knowledge Check
Two blocks each of the mass m are attached to the ends of a massless rod which pivots as shown in figure. Initially the rod is held in the horizontal position and then released. Calculate the initial angular acceleration.
 A(l2−l1)gl21+l22 clockwiseB(l2+l1)g(l22+l21) clockwiseC(l2−l1)g2(l22+l21) clockwiseDgl2+l1 clockwise
A(l2−l1)gl21+l22 clockwiseB(l2+l1)g(l22+l21) clockwiseC(l2−l1)g2(l22+l21) clockwiseDgl2+l1 clockwiseA unifrom rod of length l and mass m is free to rotate in a vertical plane about A as shown in Fig. The rod initially in horizontal position is released. The initial angular acceleration of the rod is
 A3g2lB3glCg2lD2gl
A3g2lB3glCg2lD2glIn a street light of mass M is suspended from the end of a uniform rod of length L in different possible patterns as shown in figure, then :
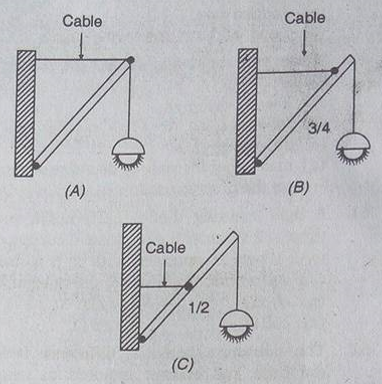 Apattern A is more sturdyBpattern B is more sturdyCpattern C is more sturdyDall will have same sturdiness
Apattern A is more sturdyBpattern B is more sturdyCpattern C is more sturdyDall will have same sturdiness
A charge Q is uniformly distributed on the rod of length L which is pivoted at one of its end. The rod is kept between two plates having charge densities o and-o. The initial angular acceleration of the rod is (mass of rod = M) + 0 o
View SolutionIn a street light of mass M is suspended from the end of a uniform rod of length L in different possible patterns as shown in figure, then :

View SolutionA rod PQ of mass M and length L is hinged at end P. The rod is kept horizontal by a massless string tied to point Q as shown in the figure. When string is cut, the initial angular accleration of the rod is.

View SolutionA rod PQ of mass M and length L is hinged at end P. The rod is kept horizontal by a massless string tied to point Q as shown in figure. When string is cut, the intial angular acceleration of the rod is

View SolutionIf asteel light of mass M is suspended from for end of a uniform rod of lkength L in diffrence possible patents as shown in figure
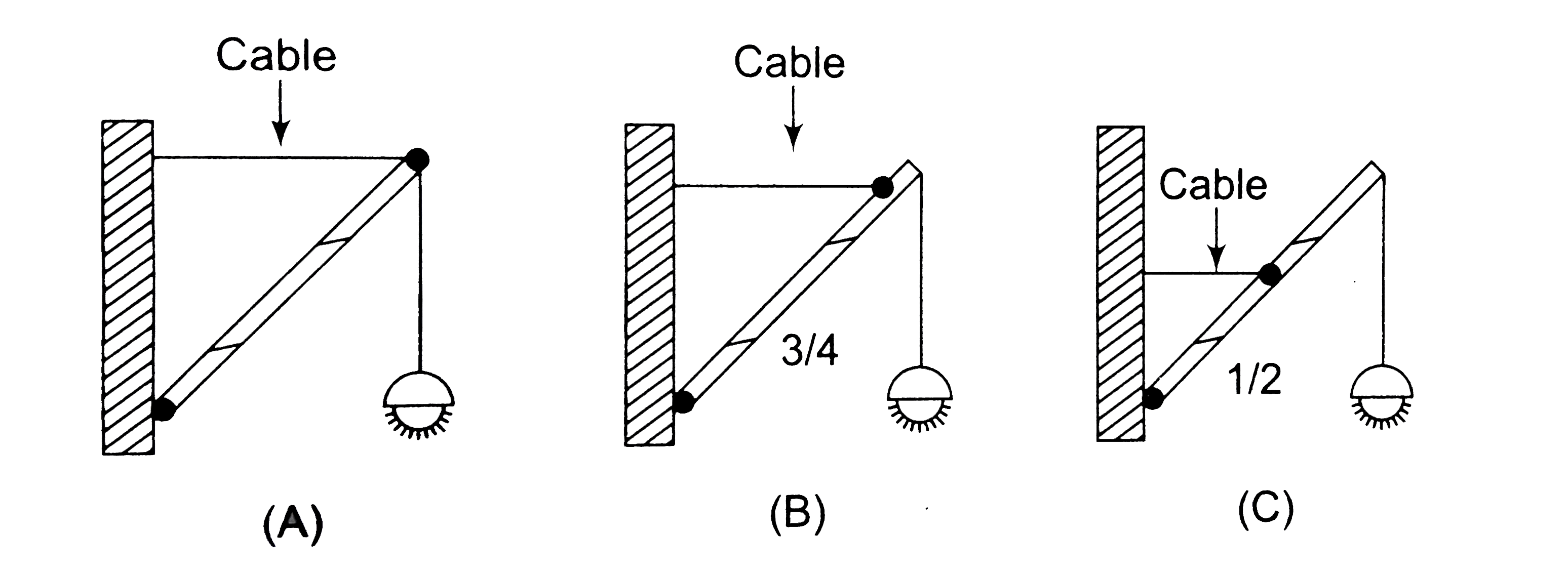
View Solution

