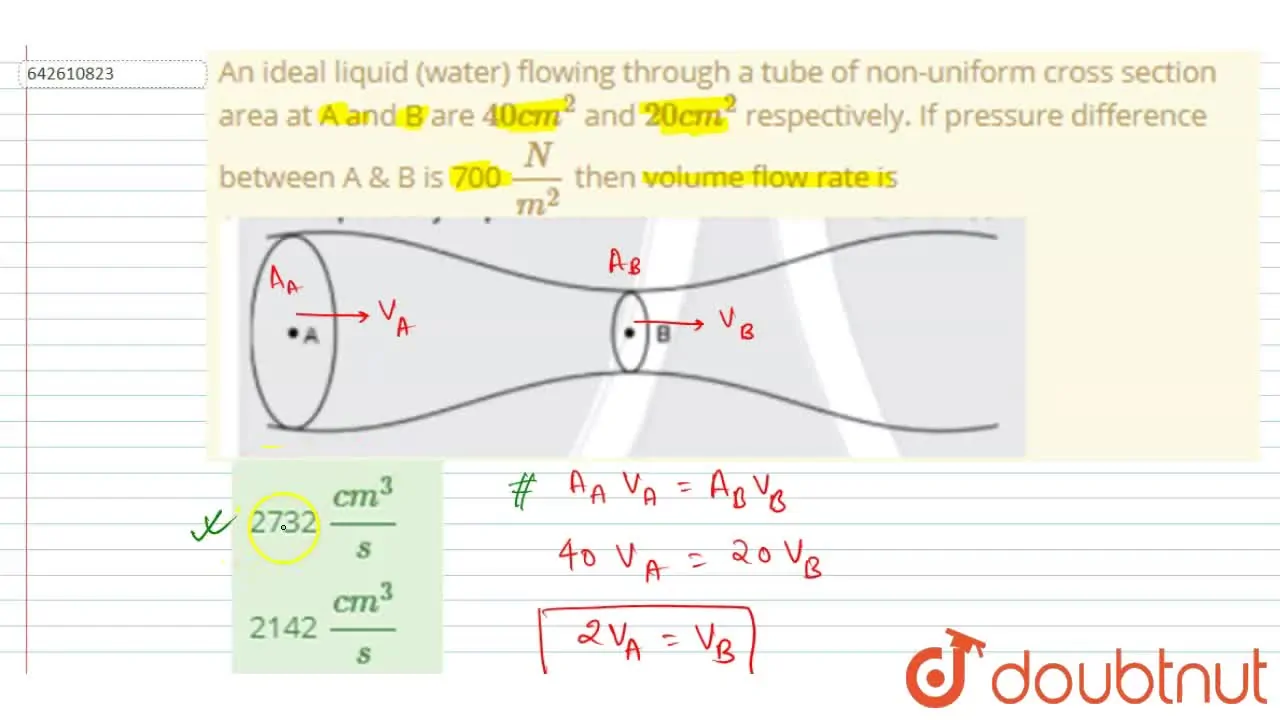
An ideal liquid (water) flowing through a tube of non-uniform cross section area at A and B are 40cm2 and 20cm2 respectively. If pressure difference between A & B is 700 Nm2 then volume flow rate is 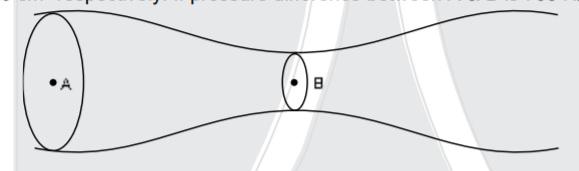
2732 cm3s
2142 cm3s
1832 cm3s
3218 cm3s
The correct Answer is:A
NA
Related Playlists
Similar Questions
Water flows through a tube shown in figure. The areas of cross section at A and B are 1cm2and0.5cm2 respectively. The height difference between A and B is 5m. If the speed of water at A is 10 cms−1 find
a) the speed at B.
b) the difference in pressures at A and B.
 View Solution
View SolutionWater flows through a tube shown in figure. The areas of cross section at A and B are 1cm2and0.5cm2 respectively. The height difference between A and B is 5cm. If the speed of water at A is 10 cms−1. Find a. the speed at B and b. the difference in pressures at A and B.
 View Solution
View SolutionThe water flowing through the same tube having two different cross section areas has different flow rates .
View SolutionWater flows through a horizontal tube of variable cross section.The area of cross section at A and B are 4 mm2and2mm2 respectively. If 1 cc of water enters per second through A find
a) The speed of water at A
b) the speed of river at B
c) the pressure difference PA−PB.
 View Solution
View SolutionWater is flowing in a non viscous tube as shown in the diagram. The diametre at a point A and B are 0.5m and 0.1m respectively. The pressure difference between points A & B are △P=0.8 then find out the rate of flow:
 View Solution
View SolutionWater flows through a horizontal tube of variable cross-section. The area of cross section at A and B are 4mm2and2mm2 respectively. If 1 cc of water enters per seconds through. A find a. The speed of water at A, b. the speed of river at B and c. the pressure difference PA−PB.
 View Solution
View SolutionA liquid is flowing through a pipe of non-uniform cross-section. At a point where area of cross-section of the pipe is less, match the following columns.
 View Solution
View SolutionWater flows through a horizontal tube as shown in figure. If the difference of height of water column in the vertical tubes in 2cm and the areas of corss-section at A and B are 4cm2 and 2cm2 respectively. Find the rate of flow of water across any section.
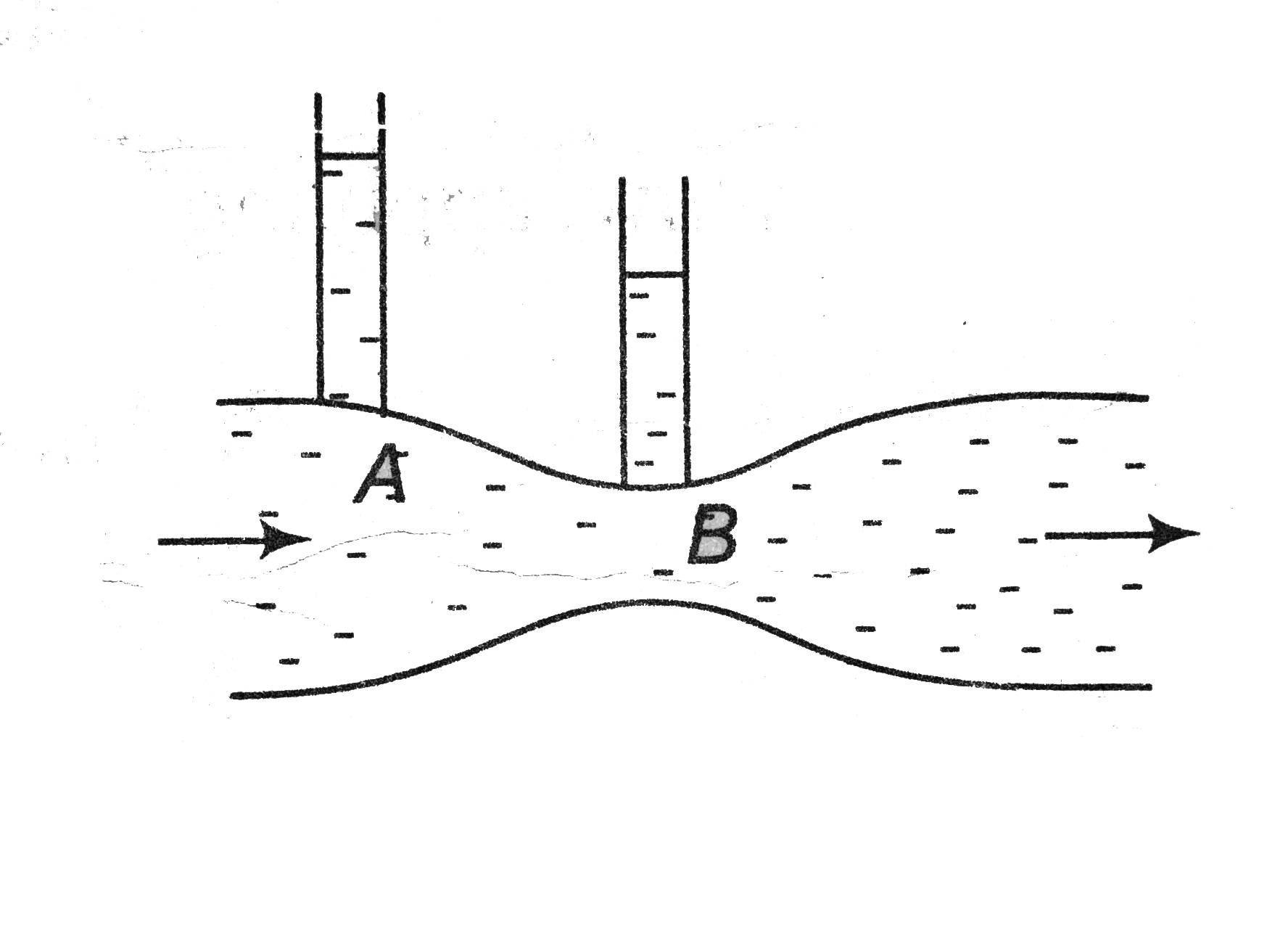 .View Solution
.View SolutionIn this figure, an ideal liquid flows through the tube having uniform area of cross-section and is held in vertical plane. Find the ratio of speed of liquid at A and B and also find the pressure difference between- these points.
 View Solution
View SolutionA pipe of non uniform cross section has two distinct section 1 and 2 with areas 2cm2 and 4cm2 respectively. If the velocity of flowing liquid at section 1 is 5cm/s, determine the velocity at section 2.
View Solution