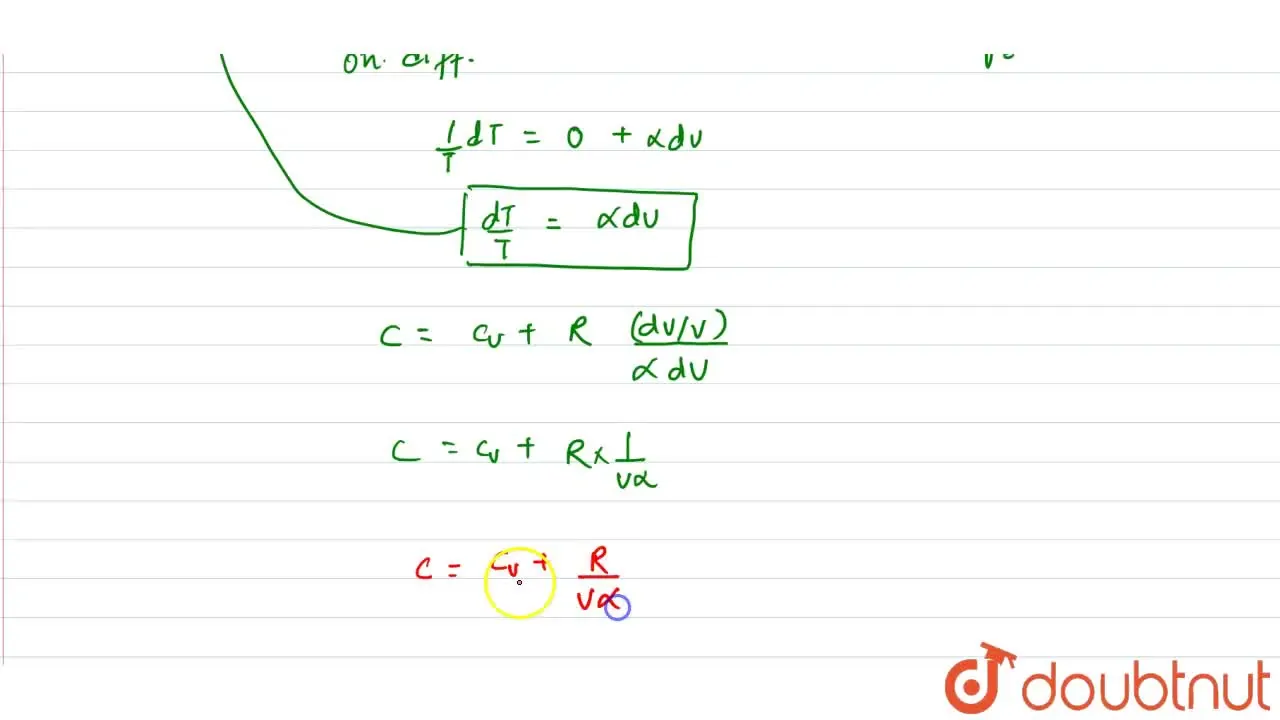
An ideal gas is made to undergo a process T=T0eαV where T0 and α are constants. Find the molar specific heat capacity of the gas in the process if its molar specific heat capacity at constant volume is Cv. Express your answer as a function of volume (V).
By first law of thermodymanics
Q=dU+W
⇒nCdT=nCVdT+PdV
⇒C=CV=PdVndT=CV+RTVdVdT
⇒C=CV+R(dV/VdT/T) . . . (i)
Process equation is given as
T=T0eαV . . . . (ii)
Tke log of equation (ii), we get
log T=log T0+αV ltBrgt ⇒dTT=0+α dV (Differentiating)
⇒dTT(dV)=α
⇒C=CV+RdV(VdTT)=CV=RdVV.αdV=CV+RαV
⇒C=CV+RαV.
Related Playlists
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Try Youself13videos
THERMODYNAMICS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Assignment (Section-A) Objective Type Questions (one option is correct)50videos
THERMODYNAMICS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Assignment (Section-J) Akash Challengers Questions7videos
THERMAL PROPERTIES OF MATTER
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - UNITS AND MEASUREMENTSEXERCISE - ASSIGNMENT (SECTION - D)15videos
UNITS AND MEASUREMENTS
Similar Questions
What is the molar specific heat capacity of a gas undergoing an adiabatic process ?
View SolutionAn ideal gas having molar specific heat capaicty at constatnt volume is 32R, the molar specific heat capacities at constant pressure is
View SolutionMolar heat capacity of gas whose molar heat capacity at constant volume is CV, for process P=2e2Vis :
View SolutionThe molar heat capacity for a gas at constant T and P is
View SolutionFor an ideal gas Cp,mCv,m=γ. The molecular mass of the gas is M, its specific heat capacity at constant volume is :
View SolutionFind the molar specific heat of the process p=aT for a monoatomic gas, a being constant.
View SolutionFind the value of molar heat capacity for an ideal gas in an adiabatic process.
View SolutionAn ideal has undergoes a polytropic given by equation PVn = constant. If molar heat capacity of gas during this process is arithmetic mean of its molar heat capacity at constant pressure and constant volume then value of n is
View Solutionan ideal diatomic gas undergoes a polytropic process described by the equation P√V=constant . The molar heat capacity of the gas during this process is
View SolutionFor an ideal gas , the specific heat at constant pressure Cp is greater than the specific heat at constant volume Cv This is because
View Solution