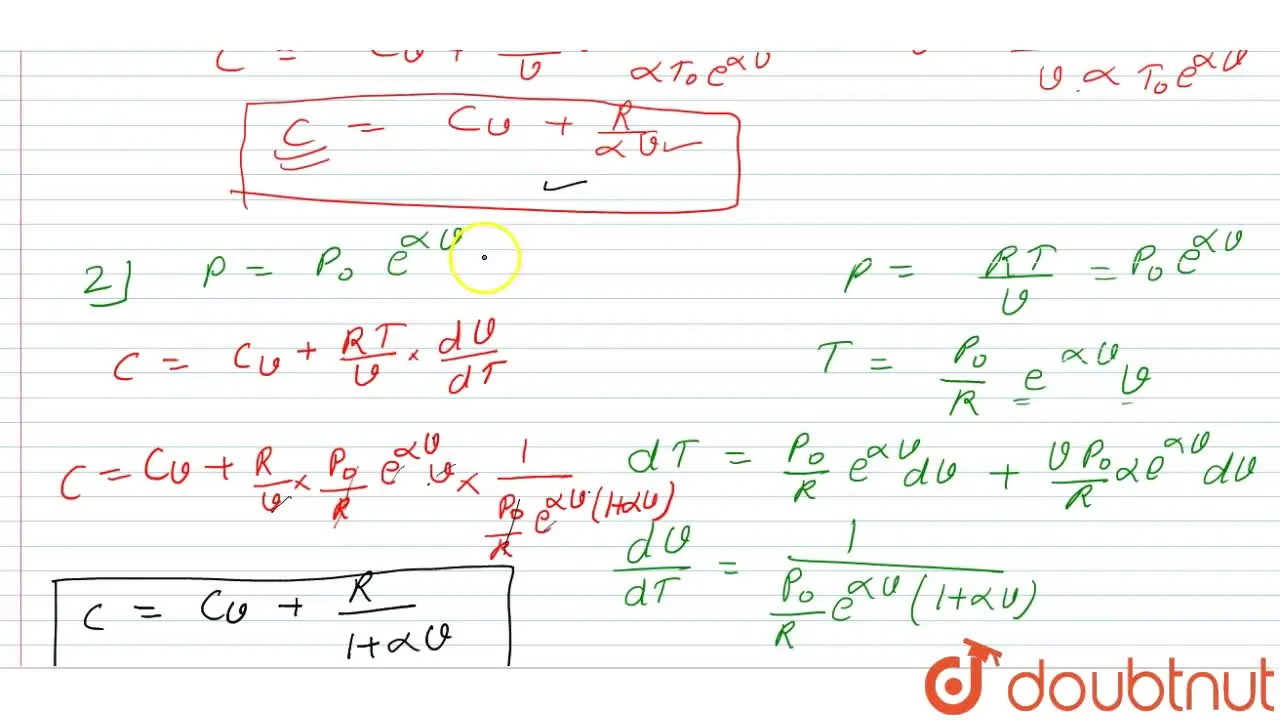
An ideal gas has a molar heat capacity at constant volume. Find the molar heat capacity of this gas as a function of its volume , if the gas undergoes the following process :
(a) ,
(b) ,
where , and are constants.
(a) By the first law of thermodynamics
Molar specfic heat according to definition
=,
We have
After differentiating, we get
So, ,
Hence
(b) Process is
or,
So, .
Related Playlists
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Kinetic Theory Of Gases51videos
THERMODYNAMICS AND MOLECULAR PHYSICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - The Second Law Of Thermodynamics - Entropy47videos
THERMODYNAMICS AND MOLECULAR PHYSICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Transport Phenomena38videos
THERMODYNAMICS AND MOLECULAR PHYSICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics49videos
PHYSICAL FUNDAMENTALS OF MECHANICS
Similar Questions
The molar heat capacity for a gas at constant T and P is
View SolutionThe molar heat capacity for a gas at constant T and P is
View SolutionFind the maximum attainable temperature of ideal gas in each of the following process :
(a) p=p0−αV2 ,
(b) p=p0e−βv,
where p0,α and β are positive constants, and V is the volume of one mole of gas.View SolutionMolar heat capacity of gas whose molar heat capacity at constant volume is CV, for process P=2e2Vis :
View SolutionFor an ideal gas the molar heat capacity varies as C=CV+3aT2. Find the equation of the process in the variables (T,V) where a is a constant.
View SolutionAn ideal gas is made to undergo a termodynamic process given by V∝T2 , find the molar heat capacity of the gas for the above process.
View SolutionFor an ideal monoatomic gas, molar heat capacity at constant volume (Cv) is
View SolutionCvandCp denote the molar specific heat capacities of a gas at costant volume and constant pressure, respectively. Then
View SolutionOne mole of an ideal gas undergoes a process such that P∝1T. The molar heat capacity of this process is 4R.
View SolutionOne mole of an ideal gas with adiabatic exponent γ undergoes the process
(a) P=P0+αV
(b) T=T0+αV
Find Molar heat capacity of the gas as a function of its volume.View Solution