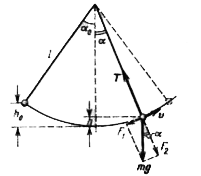
A weight of mass m hangs on a thread. The thread is deflected by an angle α0 and let go. Find the tension of the thread as a function of the angle α .
The correct Answer is:mg(3cosα−2cosα0)
In the direction normal to the velocity the forces acting on the weight are the tension of the thread T and the component of the force of gravity, F2=mgcosα (Fig. ). According to Newton.s second law
T−F2=mv2/l
To find the velocity apply the law of conservation of energy
mgh0=mgh+mv2/2
Hence
T=mgcosα+2mgl(h0−h)
However , h0=1(1−cosα0),h=l(1−cosα), therefore h0−h=l(cosα0−cosα0)
Substituting into the expression for the tension of the thread we obtain
T=mg(3cosα−2cosα0)
Similar Questions
A block of mass M lies on a plane inclined at an angle α to the horizontal. A wieght a mass m is connected to the block by a thread slung over a pulley (Fig.).
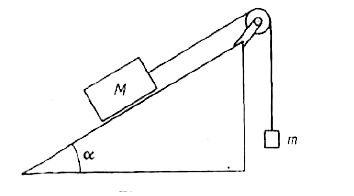
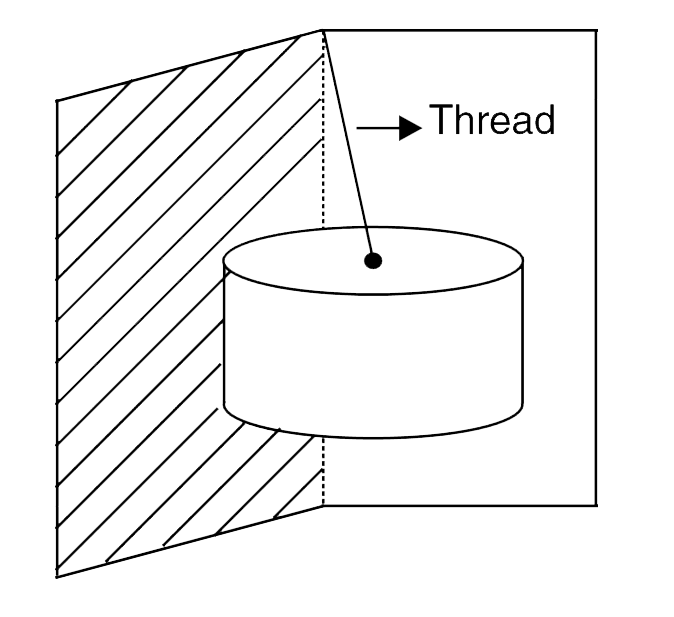
Find the acceleration of the weight and the tension of the thread. Friction, the mass of the pulley and of the thread are to be neglected.View SolutionA cylinder of mass M and radius r is suspended at the corner of a room. Length of the thread is twice the radius of the cylinder. Find the tension in the thread and normal force applied by each wall on the cylinder assuming the walls to be smooth.
 View Solution
View SolutionA cylinder of mass M and radius r is suspended at the corner of a room. Length of the thread is twice the radius of the cylinder. Find the tension in the thread and normal force applied by each wall on the cylinder assuming the walls to be smooth.
 View Solution
View SolutionA small sphere of mass m suspended by a thread is first taken aside so that the thread forms the right angle with the vertical and then released. Find:
(a) the total acceleration of the sphere and the thread tension as a function of θ, the angle of deflection of the thread from the vertical,
(b) the thread tension at the moment when the vertical component of the sphere's velocity is maximum,
(c) the angle θ between the thread and the vertical at the moment when the total acceleration vector of the sphere is directed horizontally.View Solutiona small sphere of mass m susopended by a thread is first taken aside so that the thread forms the right angle with the verticle and then realease. (a) find the total acceleration of the sphere and the thread tension as a function of θ, the angle of deflection of the thread from the vertical. (b) Find the angle θ between the thread and the vertical. at the moment when the total acceleration vector of the sphere is directed (i) horizontally (ii)vertically upward and (iii) vertically downward.
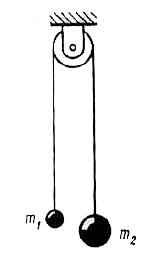
View SolutionTwo weights with masses m1andm2 are suspended from a thread slung over a pulley (Fig.). Find the acceleration of the system a1 the tension of the thread F and the force Fp acting on the pulley's axis. Neglect the mass of the thread and of the pulley and friction.
 View Solution
View SolutionA small body of mass m tied to a non-stretchable thread moves over a smooth horizontal plane. The other end of the thread is being drawn into a hole O(figure) with a constant velocity. Find the thread tension as a function of the distance r between the body and the hole if at r=r0 the angular velocity of the thread is equal to ω0.
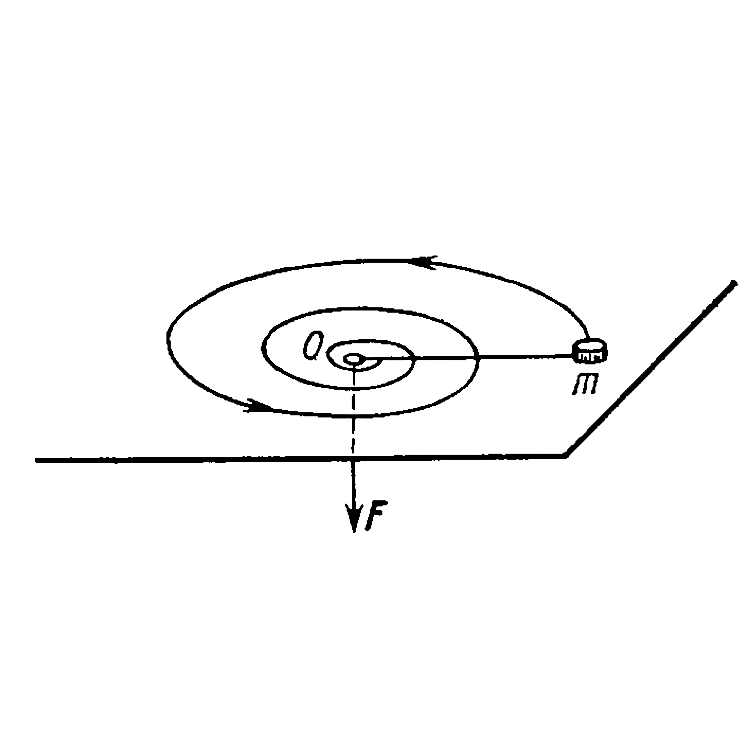 View Solution
View SolutionA spool with a thread wound on it is placed on an inclined smooth plane set an angle α=30∘ to the horizontal. The free end of the thread is attached to the wall as shown in figure. The mass of the spool is m=200g, its moment of inertia relative to its own axis I=0.45g⋅m2, the radius of the wound thread layer r=3.0cm. Find the acceleration of the spool axis.
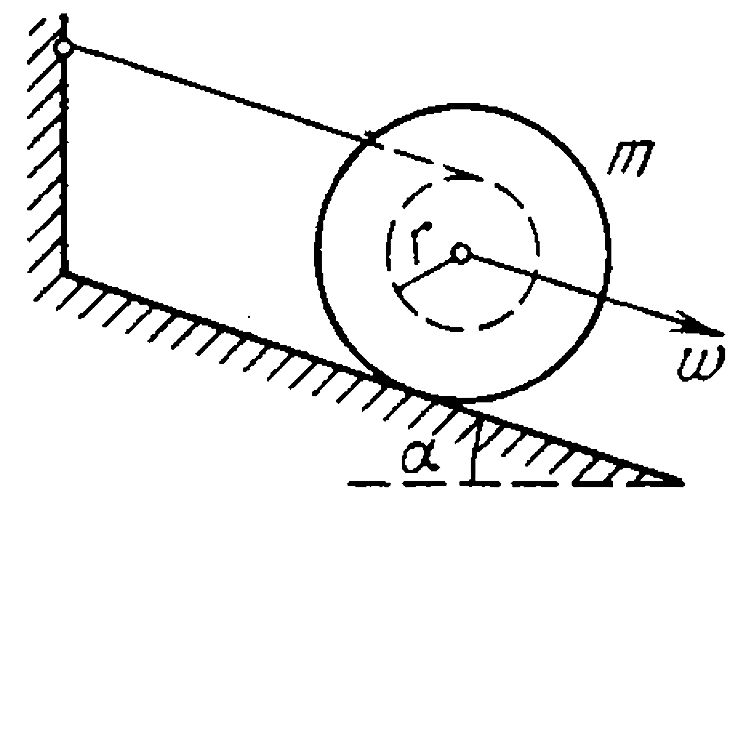 View Solution
View SolutionA cylinder of mass 0.6kg and radius R is falling under gravity without slipping as the thread is unfolding.Find the tension in the thread (in newton).
View SolutionA kite is flying, attached to a thread which is 165m long. The thread makes an angle of 30∘ with the ground. Find the height of the kite from the ground , assuming that there is no slack in the thread.
View Solution

